Students often wonder why many chemical reactions yield an equilibrium mixture in which a significant amount of the reactants are present, even though the products have a lower standard free energy than the reactants. One might at first think that as long as any reactants are present, the free energy could be reduced if conversion of reactants to products were complete.
The short answer is that by "contaminating" some of the product with reactants, the free energy of the system can be reduced below that of the pure products. This additional drop in the free energy is due to the free energy of mixing of reactants with products.
Unless you are enrolled in a more advanced course, you are probably not expected to know how to calculate free energies of mixing. All you really need to know is that it is formally equivalent to the expansion of gases (or to the dilution of a solute) into a larger volume. See here for more details.
This example illustrates how the free energies of the reaction components combine with the free energies of mixing reactants with products to minimize the Gibbs function in the equilibrium mixture. To keep things as simple as possible, we will deal with the isomerization equilibrium between the two butanes C4H10 at 298 K:
![]()
| n-butane | iso-butane | |
| S°, J mol–1 | 310 | 295 |
| ΔGf°, kJ mol–1 | –15.71 | –17.97 |
1 Calculate the mole fraction of each gas present at equilibrium.
ΔG° = ΔG°f(products) – ΔG°f(reactants) = (–17.97) – (–15.71) = –2.26 kJ mol–1.
Kp = exp(–ΔG°/(RT)) = exp(–(–2260)/(8.314 x 298)) = e.91 = 2.49
Because partial pressures are proportional to mole fractions, we can write
Kp = Kx = xiso /xn = xiso /(1–xiso) = 2.49
Solving for xiso yields xiso = .714, xn = .286
(Recall that the mole fractions in a mixture must add to unity.)
In order to keep the numbers a little simpler, let's define all of our free energies in relation to that of the pure reactant. So from now on, ΔG°n = 0.
This is just the free energy difference we calculated above:
(–17.97) – (–15.71) = –2.26 kJ mol–1
So if one mole of n-butane could be converted to one mole of the more stable iso-butane, the free energy would fall by 2260 J.

But if iso-butane is more stable, why does it make up only 77 percent of the equilibrium mixture? Why doesn't the reaction go all the way?
 Think of each gas as being in a separate compartment, each contributing an amount to the free energy in proportion to its mole fraction in the equilibrium mixture. Remember that ΔG°n has been set to zero.
Think of each gas as being in a separate compartment, each contributing an amount to the free energy in proportion to its mole fraction in the equilibrium mixture. Remember that ΔG°n has been set to zero.
(0 × .286) + (–2.26 kJ mol–1 × .714) = – 1.61 kJ mol–1
 Now suppose we remove the partition, allowing the two gases to mix without any change in the overall composition.
Now suppose we remove the partition, allowing the two gases to mix without any change in the overall composition.
This will be the free energy of mixing the respective mole fractions of the two gases.
ΔGmixing = –RT Σ(xi ln xi) = –(8.314 × 298)(.286 ln .286 + .714 ln .714)
= –(2488 J mol–1) ( –.258 – .240) = –1480 J mol–1
[Unless you are in an advanced course, don't worry about where this formula comes from.]
Just add the free energy of mixing to the free energies of the indicated numbers of moles of the two gases. This can be found simply by adding the two values calculated immediately above, but here it is worked out explicitly:
ΔGmixture = ΔGmixing + Σxi ΔG°f(i) =
(–1480) + (.286 × 0 ) + (.714 × –2260) J mol–1 = –3090 J mol–1
Gn = 0 + RT ln xn = (2488 J mol–1)(ln .286) = –3110 J mol–1
Giso = Giso° + RT ln xiso = –2260 + (2488 J mol–1)(ln .714) = –3100 J mol–1
Allowing for a bit of rounding error, these numbers are the same. This should come as no surprise: you know that the free energies of the reactants and products must be identical at equilibrium.
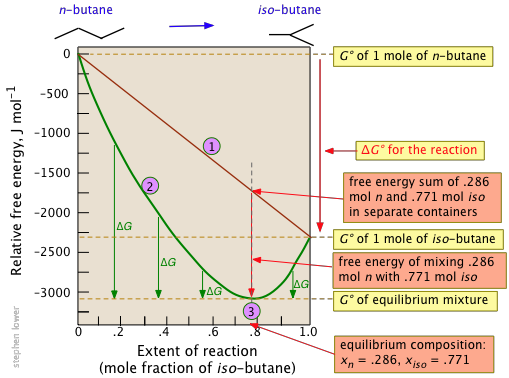
Notice particularly that
- The sum of the free energies of the two gases (n-butane and iso-butane) separately varies linearly with the composition of the mixture (red line).
- The purple curve adds the free energy of mixing to the above sum; its minimum defines the equilibrium composition.
- As the composition approaches the equilibrium value, ΔG (which denotes how much farther the free energy of the system can fall) appraches zero.
Free energies of mixing of products with reactants tend to be rather small, so for reactions having ΔG° values that are highly negative or positive (±20 kJ mol–1, say), the equilibrium mixture will, for all practical purposes, be either [almost] "pure" reactants or products.
Page last modified: 30.08.2011

