
In principle, the concentrations of all species in a monoprotic acid-base system can be found by solving the appropriate cubic equation. Although simplifications are often possible that reduce this to a quadratic or sometimes only a first-order equation, there is still an element of mathematical complexity that tends to get in the way of a real understanding of what is going on in such a solution.
There is an alternative method that, while lacking precision, affords one a far clearer view of the relationships between the various species related to a given acid-base system. This starts out with the graph shown in Fig 1..

This graph is no more than a definition of pH and pOH; for example, when the pH is 4, –log [H<sub>3</sub>O<sup>+</sup>] = 4$. (Notice that the ordinate is the negative of the log concentration, so the smaller numbers near the top of the scale refer to larger concentrations.)
The above graph of is of no use by itself, but it forms the basis for the construction of other graphs specific to a given acid-base system. For example, suppose that we want to see how the species concentrations vary with pH in a 0.001 solution of acetic acid, K<sub>a</sub> = 10<sup>–4.74</sup>}$. The graph in Fig. 2 describes this system.
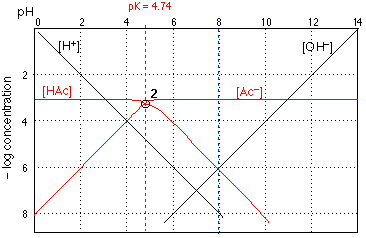
The H<sub>3</sub>O>sup>+</sup> and OH<sup>–</sup> log concentration lines are the same ones that we saw in Fig. 1. The other two lines show how the concentrations of CH<sub>3</sub>COOH ("HAc") and of the the acetate ion vary with the pH of the solution.
How do we construct the plots for [HAc] and [Ac$^{-}$]? If you look carefully at \figref{AB11}a, you will observe that each line is horizontal at the top, and then bends to become diagonal. There are thus three parameters that define these two lines: the ocation of their top, horizontal parts, their crossing points with the other lines, and the slopes of their diagonal parts.
The horizonal sections of these lines are placed at 3 on the ordinate scale, corresponding to the nominal acid concentration of 10<sup>–3</sup>. This value corresponds to
C<sub>a</sub> = [HAc] + [Ac<sup>–</sup>]
which you will recognize as the mass balance condition saying that "acetate" is conserved; C<sub>a</sub>\ is the nominal "acid concentration" of the solution, and is to be distinguished from the concentration of the actual acidic species HAc.
At low pH values (strongly acidic solution) the acetate species is completely protonated, so [HAc] = 10<sup>–3</sup> and $\rm [Ac<sup>–</sup>]=0. Similarly, at high pH, $–log \rm [Ac<sup>–</sup>]=3$ and $\rm [HAc]=0$. If the solution had some other nominal concentration, such as 0.1\molar\ or $10^{-5}$\molar, we would simply move the pair of lines up or down.
The diagonal parts of the lines have slopes of equal magnitude but opposite sign. It C<sub>a</sub>n easily be shown that these slopes d–log [HAc]}/d{\rm pH}$ etc.\ are +-1, corresponding to the slopes of the [OH<sup>–</sup>]\ and [H<sub>3</sub>O<sup>+</sup>]\ lines. Using the latter as a guide, the diagonal portions of lines 3 and 4 C<sub>a</sub>n easily be drawn.
The crossing point of the plots for the acid and base forms corresponds to the condition $\rm [HAc]=[\Ac]$. You already know that this condition holds when the pH is the same as the \pka\ of the acid, so the the pH coordinate of the crossing point must be 4.75 for acetic acid. The vertiC<sub>a</sub>l loC<sub>a</sub>tion of the crossing point is found as follows: When $\rm [HAc]= [\Ac]$, the concentration of each species must be $\half \C<sub>a</sub>$, or in this C<sub>a</sub>se 0.0005\molar . The logarithm of $\half$ is 0.3, so a 50\% reduction in the concentration of a species (from an initial value of \C<sub>a</sub> ) will shift its loC<sub>a</sub>tion down on the log concentration sC<sub>a</sub>le by 0.3 unit. The crossing point therefore falls at a log-$C$ value of $(-3) - .3 = -3.3$,
Fig 3
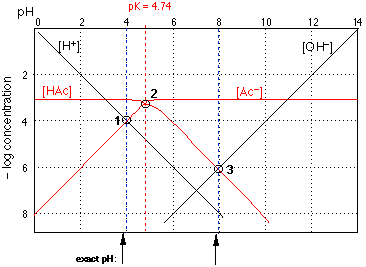 Text
Text
Fig 4
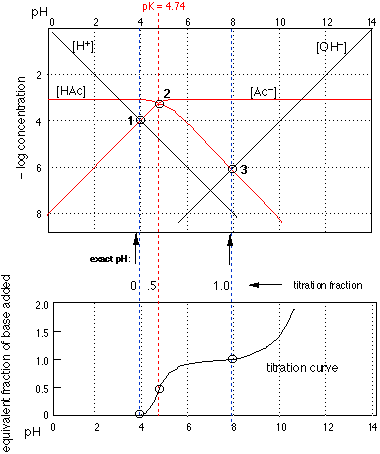 text
text
Fig 5 - a diprotic acid: oxalic acid
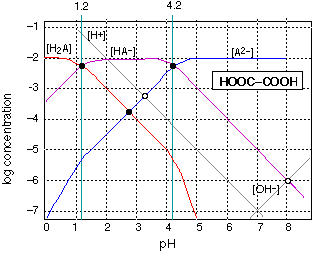
Fig 6 - Solution of ammonium formate in water
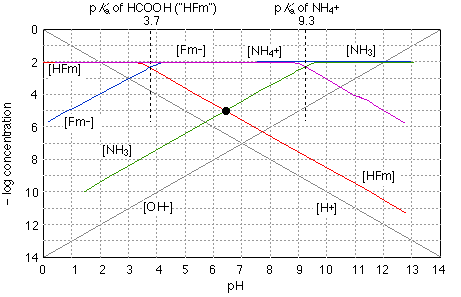
Fig 7 - ab18 - phosphate system
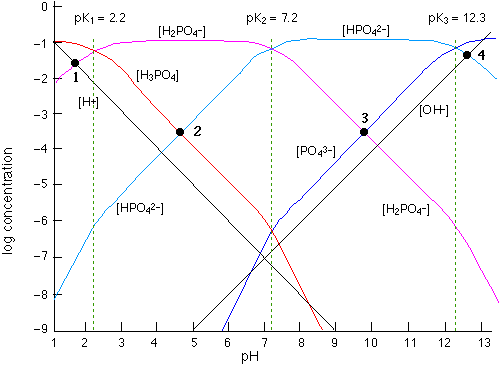
Fig 8 - the carbonate system
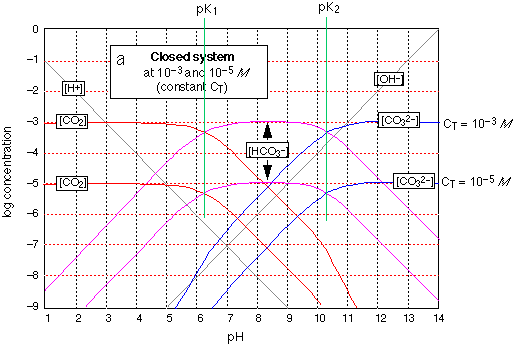
Fig 9 - glycine

Fig 10- seawater
