Observable properties of gases
Introduction to gases
Throughout much of human history, “airs” or gases were not believed to be matter at all; their apparently weightless nature and their ability to move about freely and fill all available space, while carrying with them definite physical properties such as odor and sometimes color, conferred upon them a somewhat mysterious nature. Even the scientist Robert Boyle wrote about “The Strange Subtility, Great Efficacy and Determinate Nature of Effluviums"
It's interesting, however, that around 550 BCE the Greek philosopher Anaximenes maintained that all matter consists of air: "It is from air that all the things that exist, have existed, or will exist come into being."
The invention of the sensitive balance in the early seventeenth century showed once and for all that gases have weight and are therefore matter. Guericke's invention of the air pump (which led directly to his discovery of the vacuum) launched the “pneumatic era" of chemistry long before the existence of atoms and molecules had been accepted. Indeed, the behavior of gases was soon to prove an invaluable tool in the development of the atomic theory of matter.
The study of gases allows us to understand the behavior of matter at its simplest: individual particles, acting independently, almost completely uncomplicated by interactions and interferences between each other. Later on, our knowledge of gases will serve as the pathway to our understanding of the far more complicated condensed phases (liquids and solids) in which the theory of gases will no longer give us correct answers, but it will still provide us with a useful model that will at least help us to rationalize the behavior of these more complicated states of matter.
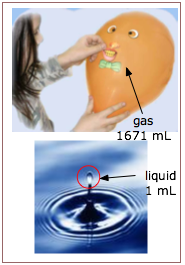
First, we know that a gas has no definite volume or shape; a gas will fill whatever volume is available to it. Contrast this to the behavior of a liquid, which always has a distinct upper surface when its volume is less than that of the space it occupies.
The other outstanding characteristic of gases is their low densities, compared with those of liquids and solids. One mole of liquid water at 298 K and 1 atm pressure occupies a volume of 18.8 cm3, whereas the same quantity of water vapor at the same temperature and pressure has a volume of 30200 cm3, more than 1000 times greater.
The most remarkable property of gases, however, is that to a very good approximation, they all behave the same way in response to changes in temperature and pressure, expanding or contracting by predictable amounts. This is very different from the behavior of liquids or solids, in which the properties of each particular substance must be determined individually.
We will see later that each of these three macroscopic characteristics of gases follows directly from the microscopic view— that is, from the atomic nature of matter.
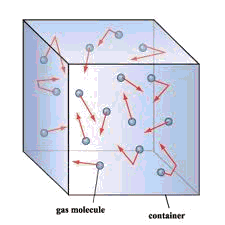
For some deeper insight into the meaning of pressure, see John Denker's page A Fluid Has Pressure Everywhere
The molecules of a gas, being in continuous motion, frequently strike the inner walls of their container. As they do so, they immediately bounce off without loss of kinetic energy, but the reversal of direction (acceleration) imparts a force to the container walls. This force, divided by the total surface area on which it acts, is the pressure of the gas.
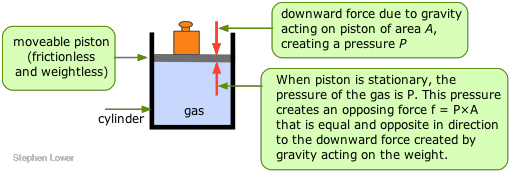
The pressure of a gas is observed by measuring the pressure that must be applied externally in order to keep the gas from expanding or contracting. To visualize this, imagine some gas trapped in a cylinder having one end enclosed by a freely moving piston. In order to keep the gas in the container, a certain amount of weight (more precisely, a force, f ) must be placed on the piston so as to exactly balance the force exerted by the gas on the bottom of the piston, and tending to push it up. The pressure of the gas is simply the quotient f/A, where A is the cross-section area of the piston.
Pressure units
The unit of pressure in the SI system is the pascal (Pa), defined as a force of one newton per square metre (1 Nm–2 = 1 kg m–1 s–2.)
At the Earth's surface, the force of gravity acting on a 1 kg mass is 9.81 N. Thus if, in the illustration above, the weight is 1 kg and the surface area of the piston is 1 M2, the pressure of the gas would be 9.81 Pa. A 1-gram weight acting on a piston of 1 cm2 cross-section would exert a pressure of 98.1 pA. (If you wonder why the pressure is higher in the second example, consider the number of cm2 contained in 1 m2.)
In chemistry, it is more common to express pressures in units of atmospheres or torr: 1 atm = 101325 Pa = 760 torr.
The older unit millimetre of mercury (mm Hg) is almost the same as the torr; it is defined as one mm of level difference in a mercury barometer at 0°C. In meteorology, the pressure unit most commonly used is the bar:
1 bar = 105 N m–2 = 750.06 torr = 0.987 atm.
In engineering work the pound per square inch is still widely used; standard atmospheric pressure is 14.7 psi. For the definition of the standard atmosphere, see here.
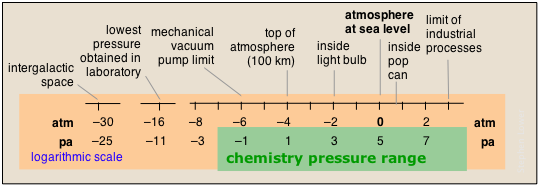
The pressures of gases encountered in nature span an exceptionally wide range, only part of which is ordinarily encountered in chemistry. Note that in the chart below, the pressure scales are logarithmic; thus 0 on the atm scale means 100 = 1 atm.
Atmospheric pressure and the barometer
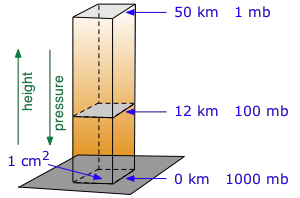
The surface pressure of 1034 g cm–2 is obtained by solving Newton's law f = ma for m, using the acceleration of gravity for a:
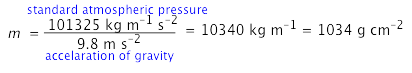
Table of atmospheric pressure by elevation - go here for elevation of your US city
So, if this huge column of air are constantly pressing down on your body, why do you not feel it?
Answer: because every other part of your body (including within your lungs and insides) also experiences the same pressure, so there is no net force (other than gravity) acting on you.
The discovery of atmospheric pressure
This was the crucial first step that led eventually to the concept of gases and their essential role in the early development of Chemistry.
In the early 17th century the Italian Evangelista Torricelli invented a device — the barometer — to measure the pressure of the atmosphere. A few years later, the German scientist and some-time mayor of Magdeburg Otto von Guericke devised a method of pumping the air out of a container, thus creating which might be considered the opposite of air: the vacuum.
As with so many advances in science, idea of a vacuum — a region of nothingness — was not immediately accepted; see here for an interesting account of the controversy.
Torricelli's invention overturned the then-common belief that air (and by extension, all gases) are weightless.
The fact that we live at the bottom of a sea of air was most spectacularly demonstrated in 1654, when two teams of eight horses were unable to pull apart two 14-inch copper hemispheres (the "Magdeburg hemispheres") which had been joined together and then evacuated with Guericke's newly-invented vacuum pump.
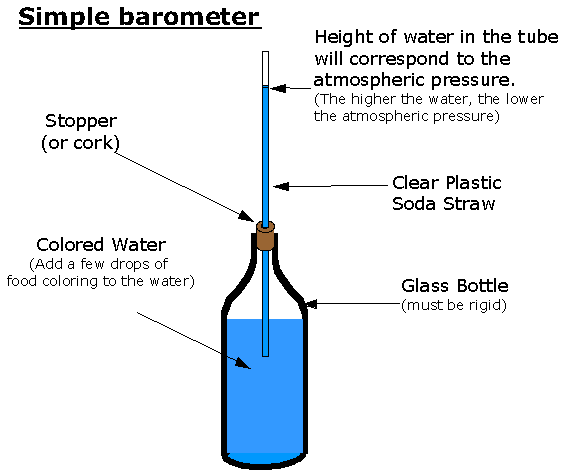
Measurement of atmospheric pressure: the barometer
The classical barometer, still used for the most accurate work, measures the height of a column of liquid that can be supported by the atmosphere. As indicated below, this pressure is exerted directly on the liquid in the reservoir, and is transmitted hydrostatically to the liquid in the column.
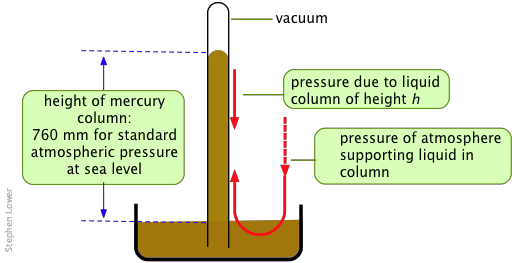
Metallic mercury, being a liquid of exceptionally high density and low vapor pressure, is the ideal barometric fluid. Its widespread use gave rise to the "millimeter of mercury" (now usually referred to as the "torr") as a measure of pressure.
How is the air pressure of 1034 g cm–3 related to the 760-mm height of the mercury column in the barometer? What if water were used in place of mercury?
Answer: The density of Hg is 13.6 g cm–3, so in a column of 1-cm2 cross-section, the height needed to counter the atmospheric pressure would be (1034 g × 1 cm2) / (13.6 g cm–3) = 76 cm.
The density of water is only 1/13.6 that of mercury, so standard atmospheric pressure would support a water column whose height is 13.6 x 76 cm = 1034 cm, or 10.3 m. You would have to read a water barometer from a fourth-story window!
left: A water-barometer (set up on the building on the right) by von Guericke in the 17th century.
right: The Thames Water Barometer is probably the most spectacular one in the world. It was built in 1995 in a London roundabout to conceal a surge standpipe for the local water distribution system.
Water barometers were once employed to measure the height of the ground and the heights of buildings before more modern methods were adopted.
←↓ Click on green-outlined images to enlarge them
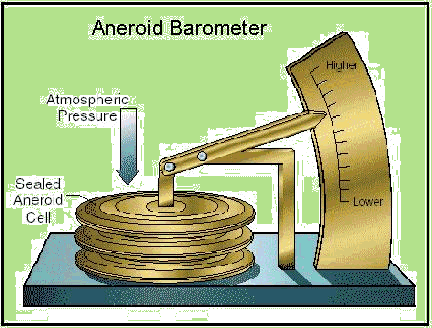
Barometers take many forms!
1
2
3
4
5
1 Aneroid barometers employ a sealed bellows which moves a pointer, as in 2 [image].
3 When the children retreat inside and the old lady emerges, the Weather Bureau predicts inclement weather.
4 Small water barometers such as this one register only variations in the pressure; the swan's body is open to the air.
5 Build-your-own water barometer to follow changes in the barometric pressure.
The manometer
This Davidson College page has a very good treatment of pressure measurement with a manometer, with simulations. And this manufacturer's site surveys the many kinds of devices used to measure the pressure of gases in practical applications.
A modification of the barometer, the U-tube manometer, provides a simple device for measuring the pressure of any gas in a container. The U-tube is partially filled with mercury, one end is connected to container, while the other end can either be opened to the atmosphere. The pressure inside the container is found from the difference in height between the mercury in the two sides of the U-tube. The illustration below shows how the two kinds of manometer work.
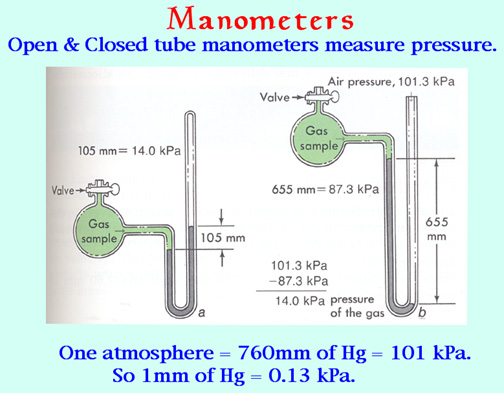[source]
The manometers ordinarily seen in the laboratory come in two flavors: closed-tube and open-tube. In the closed-tube unit shown at the left, the longer limb of the J-tube is evacuated by filling it with mercury and then inverting it. If the sample container is also evacuated, the mercury level will be the same in both limbs. When gas is let into the container, its pressure pushes the mercury down on one side and up on the other; the difference in levels is the pressure in torr.
In the open-tube manometer on the right, the atmosphere pushes the mercury column down in the open side, and again the pressure in torr is found from the difference in the levels. When using this method, the atmospheric pressure must be determined by means of a barometer.
For practical applications in engineering and industry, especially where higher pressures must be monitored, many types of mechanical and electrical pressure gauges are available.
If two bodies are at different temperatures, heat will flow from the warmer to the cooler one until their temperatures are the same. This is the principle on which thermometry is based; the temperature of an object is measured indirectly by placing a calibrated device known as a thermometer in contact with it. When thermal equilibrium is obtained, the temperature of the thermometer is the same as the temperature of the object.
Temperature scales
A thermometer makes use of some temperature-dependent quantity, such as the density of a liquid, to allow the temperature to be found indirectly through some easily measured quantity such as the length of a mercury column. The resulting scale of temperature is entirely arbitrary; it is defined by locating its zero point, and the size of the degree unit.
At one point in the 18th century, 35 different temperature scales were in use!
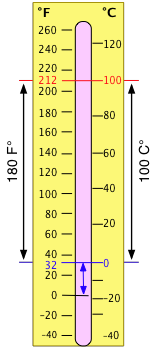
The Celsius temperature scale locates the zero point at the freezing temperature of water; the Celsius degree is defined as 1/100 of the difference between the freezing and boiling temperatures of water at 1 atm pressure.
The older Fahrenheit scale placed the zero point at the coldest temperature it was possible to obtain at the time (by mixing salt and ice.) The 100° point was set with body temperature (later found to be 98.6°F.) On this scale, water freezes at 32°F and boils at 212°F. The Fahrenheit scale is a finer one than the Celsius scale; there are 180 Fahrenheit degrees in the same temperature interval that contains 100 Celsius degrees, so 1F° = 5/9 C°. Since the zero points are also different by 32F°, conversion between temperatures expressed on the two scales requires the addition or subtraction of this offset, as well as multiplication by the ratio of the degree size.
If you take the effort to understand the above paragraph, you will never need to waste your time with formulas for converting between Fahrenheit and Celsius!
...and if you live in any country other the U.S. or Belize, you can forget about Fahrenheit altogether.
Notice also that temperature is expressed by placing the degree symbol in front of the scale abbreviation (37°C), whereas a temperature interval is written with the degree sign following the symbol (2 C°).
Absolute temperature
In 1802 the French mathematician and physicist Joseph Gay-Lussac discovered that for each Celsius degree that the temperature of a gas is lowered, the volume of the gas will diminish by 1/273 of its volume at 0°C. The obvious implication of this is that if the temperature could be reduced to –273°C, the volume of the gas would contract to zero. Of course, all real gases condense to liquids before this happens, but at sufficiently low pressures their volumes are linear functions of the temperature
(Charles' Law), and extrapolation of a plot of volume as a function of temperature predicts zero volume at -273°C. This temperature, known as absolute zero, corresponds to the total absence of thermal energy.
The temperature scale on which the zero point is –273.15°C was suggested by Lord Kelvin, and is usually known as the Kelvin scale. Since the size of the Kelvin and Celsius degrees are the same, conversion between the two scales is a simple matter of adding or subtracting 273.15; thus room temperature, 20°, is about 293 K.
A rather fine point to note: the degree symbol is not used with the "K", which should always be separated from the preceding number by a space. See here for an explanation.
Because the Kelvin scale is based on an absolute, rather than on an arbitrary zero of temperature, it plays a special significance in scientific calculations; most fundamental physical relations involving temperature are expressed mathematically in terms of absolute temperature. In engineering work, an absolute scale based on the Fahrenheit degree is sometimes used; this is known as the Rankine scale.
The volume of a gas is simply the space in which the molecules of the gas are free to move. If we have a mixture of gases, such as air, the various gases will coexist within the same volume. In these respects, gases are very different from liquids and solids, the two condensed states of matter.
The volume of a gas can be measured by trapping it above mercury in a calibrated tube known as a gas burette. The SI unit of volume is the cubic metre, but in chemistry we more commonly use the litre and the millilitre (ml). The cubic centimetre (cc) is also frequently used; it is very close to 1 milliliter (mL).
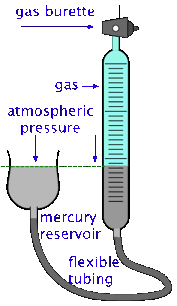
It's important to bear in mind, however, that the volume of a gas varies with both the temperature and the pressure, so reporting the volume alone is not very useful. A common practice is to measure the volume of the gas under the ambient temperature and atmospheric pressure, and then to correct the observed volume to what it would be at standard atmospheric pressure and some fixed temperature, usually 0° C or 25°C.
