Chemical Equations and Calculations

Note: this document will print in an appropriately modified format (11 pages)

A chemical equation expresses the net change in composition associated with a chemical reaction by showing the number of moles of reactants and products. But because each component has its own molar mass, equations also implicitly define the way in which the masses of products and reactants are related. In this unit we will concentrate on understanding and making use of these mass relations.

1 How to read and write chemical equations

In a chemical reaction, one or more reactants are transformed into products:

reactants → products

The purpose of a chemical equation is to express this relation in terms of the formulas of the actual reactants and products that define a particular chemical change. For example, the reaction of mercury with oxygen to produce mercuric oxide would be expressed by the equation

Hg + O₂ → HgO₂

Sometimes, for convenience, it is desirable to indicate the physical state (gas, liquid or solid) of one or more of the species by appropriate abbreviations:

Hg(l) + O₂(g) → HgO₂(s)

C(graphite) + O₂(g) → CO₂(g)

C(diamond) + O₂(g) → CO₂(g)

However, this is always optional.

Chemical equations must be balanced!

Basically, this means that chemical equations must be consistent with the law of conservation of mass:

In the context of an ordinary chemical reaction, conservation of mass means that atoms are neither created nor distroyed. This requirement is easily met by making sure that there are equal numbers of all atoms on both sides of the equation.

When we balance an equation, we simply make it consistent with the observed fact that individual atoms are conserved in chemical changes.

Problem Example 1: combustion of propane

Write a balanced equation for the combustion of propane C₃H₈ in oxygen O₂. The products are carbon dioxide CO₂ and water H₂O.

Solution: Begin by writing the unbalanced equation

C₃H₈ + O₂ → CO₂ + H₂O

It is usually best to begin by balancing compounds containing the least abundant element, so we first balance the equation for carbon:

C₃H₈ + O₂→3 CO₂ + H₂O

In balancing the oxygen, we see that there is no way that an even number of O₂ molecules on the left can yield the uneven number of O atoms shown on the right. Don't worry about this now— just use the appropriate fractional coefficient:

C₃H₈ + 3 ½ O₂ → 3 CO₂ + H₂O

Finally, we balance the hydrogens by adding more waters on the right:

C₃H₈ + 7/2 O₂ → 3 CO₂ + 4 H₂O

Ah, but now the oxygens are off again — fixing this also allows us to get rid of the fraction on the left side:

C₃H₈ + 5 O₂ → 3 CO₂ + 4 H₂O

It often happens, however, that we do end up with a fractional coefficient, as in this variant of the above example.

Problem Example 2: combustion of ethane

Write a balanced equation for the combustion of ethane C₂H₆ in oxygen O₂. The products are carbon dioxide CO₂ and water H₂O.

Solution: Begin by writing the unbalanced equation

C₂H₆ + O₂ → CO₂ + H₂O

...then balance the carbon:

C₂H₆ + O₂→2 CO₂ + H₂O

Let's balance the hydrogen next:

C₂H₆ + O₂ → 2 CO₂ + 3 H₂O

...but now we need a non-integral number of dioxygen molecules on the left:

C₂H₆ + 7/2 O₂ → 2 CO₂ + 3 H₂O

My preference is to simply leave it in this form; there is nothing wrong with 7/2 = 3 ½ moles of O₂, and little to be gained by multiplying every term by two— not unless your teacher is a real stickler for doing it "by the book", in which case you had better write

2 C₂H₆ + 7 O₂ → 4 CO₂ + 6 H₂O

2 Net ionic equations

Ionic compounds are usually dissociated in aqueous solution; thus if we combine solutions of silver nitrate AgNO₃ and sodium chloride NaCl we are really combining four different species: the cations (positive ions) Ag⁺ and Na⁺and the anions (negative ions) NO₃^– and Cl^–. It happens that when the ions Ag⁺ and Cl^– are brought together, they will combine to form an insoluble precipitate of silver chloride. The net equation for this reaction is

Ag⁺(aq) + Cl^–(aq)→ AgCl(aq)

Note that

the ions NO₃^– and Cl^– are not directly involved in this reaction; the equation expresses only the net change, which is the removal of the silver and chloride ions from the solution to form an insoluble solid.
the symbol (aq) signifies that the ions are in aqueous solution, and thus are hydrated, or attached to water molecules.
the symbol (s) indicates that the substance AgCl exists as a solid. When a solid is formed in a reaction that takes place in solution, it is known as a precipitate. The formation of a precipitate is often indicated by underscoring.

Predicting the outcome when dissolved salts are mixed

From the above example involving silver chloride, it is clear that a meaningful net ionic equation can be written only if two ions combine to form an insoluble compound. In order to make this determination, it helps to know the solubility rules— which all students of chemistry were at one time required to memorize, but are nowadays usually obtained from tables such as the one shown below.

Anion (negative ion)	Cation (positive ion)	Soluble?
any anion	alkali metal ions (Li⁺, Na⁺, K⁺, etc.)	yes
nitrate, NO₃^–	any cation	yes
acetate, CH₃COO^–	any cation except Ag⁺	yes
halide ions Cl^–, Br^–, or I^–	Ag⁺, Pb²⁺, Hg₂²⁺, Cu²⁺	no
halide ions Cl^–, Br^–, or I^–	any other cation	yes
sulfate, SO₄^2–	Ca²⁺, Sr²⁺, Ba²⁺, Ag⁺, Pb²⁺	no
sulfate, SO₄^2–	any other cation	yes
sulfide, S₂^–	alkali metal ions or NH₄⁺	yes
sulfide, S₂^–	Be²⁺, Mg²⁺, Ca²⁺, Sr²⁺, Ba²⁺, Ra²⁺	yes
sulfide, S₂^–	any other cation	no
hydroxide, OH^–	alkali metal ions or NH₄⁺	yes
hydroxide, OH^–	Sr²⁺, Ba²⁺, Ra²⁺	slightly
hydroxide, OH^–	any other cation	no
phosphate, PO₄^3–, carbonate CO₃^2–	alkali metal ions or NH₄⁺	yes
phosphate, PO₄^3–, carbonate CO₃^2–	any other cation	no

3 Mass relations in chemical equations

Basic "chemical arithmetic"

A balanced chemical equation expresses the relative number of moles of each component (product or reactant), but because each formula in the equation implies a definite mass of the substance (its molar mass), the equation also implies that certain weight relations exist between the components. For example, the equation describing the combustion of carbon monoxide to carbon dioxide

2 CO + O₂ → 2 CO₂

implies the following relations:

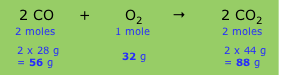
The relative masses shown in the bottom line establish the stoichiometry of the reaction, that is, the relations between the masses of the various components. Since these masses vary in direct proportion to one another, we can define what amounts to a conversion factor (sometimes referred to as a chemical factor) that relates the mass of any one component to that of any other component.

But the same relation applies to any common set of mass or weight units, so we can simply say that the mass ratio of CO₂-to-CO expressed by the above equation is 1.57, which is also just the mass ratio of these two components in the equation. This, in turn, allows us to easily handle such problems as the following:

Mastering mass-mass problems

Don't expect to pass Chemistry unless you can handle problems such as the ones below; they come up frequently in all kinds of contexts. If you feel the need for more guidance, see one of the video tutorials listed near the bottom of this page.

Problem Example 5

The ore FeS₂ can be converted into the important industrial chemical sulfuric acid H₂SO₄ by a series of processes. Assuming that the conversion is complete, how many liters of sulfuric acid (density 1.86 kg L^–1) can be made from 50 kg of ore?

Solution: As with most problems, this breaks down into several simpler ones. We begin by working out the stoichiometry on the assumption that all the sulfur in the or ends up as H₂SO₄, allowing us to write

FeS₂ → 2 H₂SO₄

Although this "skeleton" equation is incomplete (and thus not balanced), it is balanced in respect to the two components of interest, and this is all we need here. The molar masses of the two components are 120.0 and 98 g mol^–1, respectively, so the equation can be interpreted in terms of masses as

[120 mass units] FeS₂ → [2 × 98 mass units] H₂SO₄

Thus 50 kg of ore will yield (50 kg) × (196/120) = 81.7 kg of product.
[Check: is this answer reasonable? Yes, because the factor (196/120) is close to (200/120) = 5/3, so the mass of product should be slightly smaller than twice the mass of ore consumed.]

From the density information we find that the volume of liquid H₂SO₄ is

(81.7 kg) ÷ (1.86 kg L^–1) = 43.9 L
[Check: is this answer reasonable? Yes, because density tells us that the number of liters of acid will be slightly greater than half of its weight.]

Problem Example 6

Barium chloride forms a crystalline hydrate, BaCl₂·xH₂O, in which x molecules of water are incorporated into the crystalline solid for every unit of BaCl₂. This water can be driven off by heat; if 1.10 g of the hydrated salt is heated and reweighed several times until no further loss of weight (i.e., loss of water) occurs, the final weight of the sample is 0.937 g. What is the value of x in the formula of the hydrate?

Solution:

The first step is to find the number of moles of BaCl₂ (molecular weight 208.2) from the mass of the dehydrated sample.

(0.937 g) / (208.2 g mol^–1) = 0.00450 mol

Now find the moles of H₂O (molecular weight 18) lost when the sample was dried:

(1.10 – .937)g / (18 g mol^–1) = .00905 mol

Allowing for a reasonable amount of measurement error, it is apparent that the mole ratio of BaCl₂:H2O = 1:2. The formula of the hydrate is BaCl₂·2H₂O.

4 Understanding limiting reactants

Most chemical reactions that take place in the real world begin with more or less arbitrary amounts of the various reactants; we usually have to make a special effort if we want to ensure that stoichiometric amounts of the reactants are combined. This means that one or more reactant will usually be present in excess; there will be more present than can react, and some will remain after the reaction is over. At the same time, one reactant will be completely used up; we call this the limiting reactant because the amount of this substance present will control, or limit, the quantities of the other reactants that are consumed as well as the amounts of products produced.

Limiting reactant problems are handled in the same way as ordinary stoichiometry problems with one additional preliminary step: you must first determine which of the reactants is limiting— that is, which one will be completely used up. To start you off, consider the following very simple example

Problem Example 7

For the hypothetical reaction 3 A + 4 B → [products], determine which reactant will be completely consumed when we combine
a) equimolar quantities of A and B;
b) 0.57 mol of A and 0.68 mol of B.

Solution:

a) Simple inspection of the equation shows clearly that more moles of B are required, so this component will be consumed (and is thus the limiting reactant), leaving behind ¾ as many moles of A.

b) How many moles of B will react with .57 mol of A? The answer will be
(4/3 × 0.57 mol). If this comes to less than 0.68 mol, then B will be the limiting reactant, and you must continue the problem on the basis of the amount of B present. If the limiting reactant is A, then all 0.57 mol of A will react, leaving some of the B in excess. Work it out!

Problem Example 8

Sulfur and copper, when heated together, react to form copper(I) sulfide, Cu₂S. How many grams of Cu₂S can be made from 10 g of sulfur and 15 g of copper?

Solution: From the atomic weights of Cu (63.55) and S (32.06) we can interpret the he reaction 2 Cu + S → Cu₂S as

[2 × 63.55 = 127.1 mass units] Cu + [32.06 mass units] S
→ [159.2 mass units] Cu₂S

Thus 10 g of S will require (10 g S) × (127.1 g Cu)/(32.06 g S) = 39.6 g Cu
...which is a lot more than what is available, so copper is the limiting reactant here.
[Check: is this answer reasonable? Yes, because the chemical factor (127/32) works out to about 4, indicating that sulfur reacts with about four times its weight of copper.]

The mass of copper sulfide formed will be determined by the mass of copper available:

(15 g Cu) × (159.2 g Cu₂S) / (127.1 g Cu) = 18.8 g Cu₂S
[Check: is this answer reasonable? Yes, because the chemical factor (159.2/127.1) is just a bit greater than unity, indicating that the mass of the product will slightly exceed that of the copper consumed.]

Limiting reactants in everyday life

The concept of limiting reactants touches us all in our everyday lives — and as we will show in the second example below, even in the maintenance of life itself!

Air-to-fuel ratios in combustion

Combustion is an exothermic process in which a fuel is combined with oxygen; complete combustion of a hydrocarbon fuel such as methane or gasoline yields carbon dioxide and water:

CH₄ + 2 O₂ → CO₂ + 2 H₂O(g)

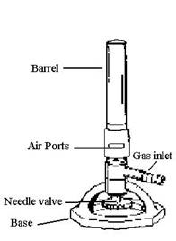
Bunsen flames Complete combustion of each kg of methane consumes 4 kg of dioxygen, which is supplied by the air. In the classic Bunsen burner, this air is admitted through an adjustable opening near the base. When it is fully open, the flame is blue in color and achieves its maximum temperature, indicating that combustion is approximately stoichiometric. If the opening is gradually closed, the appearance of the flame changes as illustrated. Under these conditions, oxygen becomes the limiting reactant and combustion is incomplete.

Incomplete combustion is generally undesirable because it wastes fuel, produces less heat, and releases pollutants such as carbon soot. Energy-producing combustion processes should always operate in fuel-limited mode.

In ordinary combustion processes, the source of oxygen is air. Because only about 20 percent of the molecules in dry air consist of O₂, the volume of air that must be supplied is five times greater than what would be required for pure O₂. Calculation of the air-to-fuel mass ratio ("A/F ratio") employed by combustion engineers is complicated by the differing molar masses of dioxygen and air. For methane combustion, the A/F ratio works out to about 17.2. (For the detailed calculation, see here). A/F ratios which exceed the stoichiometric values are said to be lean, while those in which air becomes the limiting component are characterized as rich. In order to ensure complete combustion, it is common practice to maintain a slightly lean mixture. The quantities of so-called excess air commonly admitted to burners vary from 5-10% for natural gas to up to 100% for certain grades of coal.

For internal combustion engines fueled by gasoline (roughly equivalent to
C₇H₁₄), the stoichiometric A/F ratio is 15:1. However, practical considerations necessitate differing ratios at various stages of operation. Typical values vary from a rich ratio for starting or acceleration to slightly lean ratios for ordinary driving. These ratios are set by the carburetor, with additional control by the engine computer and exhaust-line oxygen sensor in modern vehicles, or by a manual choke in earlier ones.

Aerobic and anaerobic respiration

Our bodies require a continual supply of energy in order to maintain neural activity, synthesize proteins and other essential biochemical components, replace cells, and to power muscular action. The "fuel" — the carrier of chemical energy — glucose, a simple sugar which is released as needed from the starch-like polymer glycogen, the form in which the energy we derive from food is stored.

Arterial blood carries dissolved glucose along with hemoglobin-bound dioxygen to individual cells which are the sites of glucose "combustion":

C₆H₁₂O₆ + 6 O₂ → 6 CO₂ + 6 H₂O

The net reaction and the quantity of energy released are the same as if the glucose were burned in the open air, but within the cells the reaction proceeds in a series of tiny steps which capture most of this energy for the body's use, liberating only a small fraction of it as thermal energy (heat).

Because this process utilizes oxygen from the air we breath, it is known as aerobic respiration. And as with any efficient combustion process, glucose is the limiting reactant here.

But there are times when vigorous physical activity causes muscles to consume glucose at a rate that exceeds the capacity of the blood to deliver the required quantity of oxygen. Under these conditions, cellular respiration shifts to an alternative anaerobic mode:

C₆H₁₂O₆ → 2 CH₃CH(OH)COOH

As you can see from this equation, glucose is only partially broken down (into lactic acid), and thus only part of its chemical energy is captured by the body.

There are numerous health benefits to aerobic exercise, including increased ability of the body to maintain an aerobic condition. But if you are into short-distance running (sprinting) or being pursued by a tiger, the reduced efficiency of anaerobic exercise may be a small price to pay.

Videos

Video tutorials from and other sources provide an alternative means of presenting and explaining concepts that can usefully supplement the printed word. The following are recommended for users of the present unit.

Basic reaction stoichiometry

What is stoichiometry? (VMScience, 31½ min)
Calculations from equations (SandraEtheridge, 10 min)
Stoichiometry (Khan, 10 min)
Example: oxidation of glucose (Khan, 19 min)

Limiting reactants

Limiting reactant in mole-mole calculations (utaustinchem, 4 min)
Limiting reactants, percent yield (bozemanbiology, 9 min)
Limiting reactant (IsaacsTeach, 7½ min)

What you should be able to do

Make sure you thoroughly understand the following essential ideas which have been presented above. It is especially important that you know the precise meanings of all the highlighted terms in the context of this topic.

Given the formulas of reactants and products, write a balanced chemical equation for the reaction.
Given the relative solubilities, write a balanced net ionic equation for a reaction between aqueous solutions of two ionic compounds.
Write appropriate chemical conversion factors to calculate the masses of all components of a chemical reaction when the mass of any single component is specified in any system of units.
When the masses of two or more reactants are specified, identify the limiting reactant and find the masses of all components present when the reaction is complete.
Describe the manner in which the concept of limiting reactant relates to combustion and human exercise.

Concept Map

Chemical equations and calculations

Basic chemical arithmetic and stoichiometry