The shared-electron covalent bond
Lewis dot-structures and the octet rule
The concept of the covalent bond that we present here is an essential part of the universal language of chemistry; without it, one is chemically illiterate. Fortunately, it is the easiest model to understand and to use for predicting the bonding patterns in the vast majority of molecules.
G.N. Lewis preached the gospel of shared electron-pairs to the unwashed multitudes [image]
The first really successful theory of chemical bonding was formulated by G.N.Lewis, whose 1902 lab notes eventually led to his classic article The Atom and the Molecule in 1916.

 G.N. Lewis (1875-1946) created the College of Chemistry at the University of California, Berkeley, and made it into one of the world’s most productive centers of chemistry research. His other notable work included acid-base theory, the thermodynamics of solutions, the first isolation of heavy water (D2O), and the phosphorescence and magnetic properties of molecules.
G.N. Lewis (1875-1946) created the College of Chemistry at the University of California, Berkeley, and made it into one of the world’s most productive centers of chemistry research. His other notable work included acid-base theory, the thermodynamics of solutions, the first isolation of heavy water (D2O), and the phosphorescence and magnetic properties of molecules.

Although Lewis originated the idea of the electron-pair bond, much of the credit for its early acceptance must go to Irving Langmuir, who extended it somewhat and enthusiastically popularized it to the extent that it began to be known as the Lewis-Langmuir theory, and even (to Lewis' annoyance) as the “Langmuir theory”.
Lewis and Langmuir were probably the two greatest American chemists of the first half of the twentieth century. Two interesting articles about them can be found at the Chemical Heritage Foundation site and at this Chemical Achievers site. Both scientists had earlier been involved in developing the cubical atom model which Lewis formulated in 1902 and which eventually led to the octet rule.
At the time Lewis began developing his ideas in 1902, it was widely believed that chemical bonding involved electrostatic attraction between ion-like entities. This seemed satisfactory for compounds such as NaCl that were known to dissociate into ions when dissolved in water, but it failed to explain the bonding in non-electrolytes such as CH4. Atomic orbitals had not yet been thought of, but the concept of “valence” electrons was known, and the location of the noble gases in the periodic table suggested that all except helium posses eight valence electrons. It was also realized that elements known to form simple ions such as Ca2+ or Cl– do so by losing or gaining whatever number of electrons is needed to leave eight in the valence shell of each. Lewis sought a way of achieving this octet in a way that did not involve ion formation, and he found it in his shared electron-pair theory published in 1916.
Present-day shared electron-pair theory is based on the premise that the s2p6 octet in the outermost shells of the noble gas elements above helium represents a particularly favorable configuration. This is not because of any mysterious properties of octets (or of noble gas atoms); it simply reflects the fact that filling an existing s-p valence shell is energetically more favorable than placing electrons in orbitals of higher principal quantum number. The sharing of electrons in this way between atoms means that more electrons are effectively “seeing” more nuclei, which you should remember is always the fundamental energetic basis of bond formation.
"Noble gas" valence electron configurations
The idea that the noble-gas configuration is a particularly favorable one which can be achieved through formation of electron-pair bonds with other atoms is known as the octet rule.
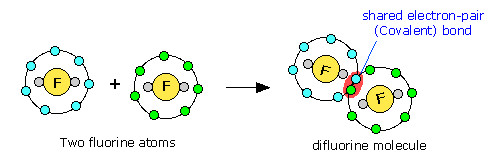
Noble gas configuration (in this case, that of neon, s2p6) is achieved when two fluorine atoms (s2p5) are able to share an electron pair, which becomes the covalent bond. Notice that only the outer (valence shell) electrons are involved.
Lewis’ idea that the electrons are shared in pairs stemmed from his observation that most molecules possess an even number of electrons. This paired sharing also allows the formulas of a large number of compounds to be rationalized and predicted— a fact that led to the widespread acceptance of the Lewis model by the early 1920s.
Scope of the octet rule
For the lightest atoms the octet rule must be modified, since the noble-gas configuration will be that of helium, which is simply s2 rather than s2p6. Thus we write LiH as Li:H, where the electrons represented by the two dots come from the 2s orbital of lithium and the 1s orbital of hydrogen.
The octet rule applies quite well to the first full row of the periodic table (Li through F), but beyond this it is generally applicable only to the non-transition elements, and even in many of these it cannot explain many of the bonding patterns that are observed. The principal difficulty is that a central atom that is bonded to more than four peripheral atoms must have more than eight electrons around it if each bond is assumed to consist of an electron pair. In these cases, we hedge the rule a bit, and euphemistically refer to the larger number of electrons as an “expanded octet”.
These situations tend to occur in atoms whose d orbitals are energetically close enough to the most highly-occupied s2p6 orbitals that they can become involved in electron-sharing with other atoms.
In spite of the octet rule’s many exceptions and limitations, the shared electron-pair model is the one that chemists most frequently employ in their day-to-day thinking about molecules. It continues to serve as a very useful guiding principle and can be a good starting point for more sophisticated theories.
The shared electron-pair is such a fundamental concept of chemical bonding that it is important to have a simple way of writing out a formula that explicitly shows the disposition of the shared pairs between the different atoms. This is commonly accomplished by depicting the valence (outermost) electrons of each bonded atom as dots that are written around the atom symbols. For example, the formation of H2 can be depicted as
H· + H· → H:H
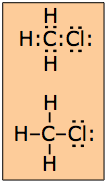 The Lewis theory makes no prediction about molecular shapes, so it is permissible to arrange the dot pairs and other atoms around the central atom in an arbitrary way that is usually governed more by esthetics than reality. It is sometimes preferable to represent an electron pair by a line: H—H which of course is the traditional way of representing a chemical bond.
The Lewis theory makes no prediction about molecular shapes, so it is permissible to arrange the dot pairs and other atoms around the central atom in an arbitrary way that is usually governed more by esthetics than reality. It is sometimes preferable to represent an electron pair by a line: H—H which of course is the traditional way of representing a chemical bond.
Bonding and nonbonding electrons: lone pairs
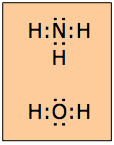 In many molecules, not all of the electron pairs comprising the octet are shared between atoms. The unshared electron pairs are often called lone pairs. Although lone pairs are not directly involved in bond formation, they should always be shown in Lewis formulas; we will see later that they have an important role to play in determining the shape of the molecule.
In many molecules, not all of the electron pairs comprising the octet are shared between atoms. The unshared electron pairs are often called lone pairs. Although lone pairs are not directly involved in bond formation, they should always be shown in Lewis formulas; we will see later that they have an important role to play in determining the shape of the molecule.
Multiple bonds
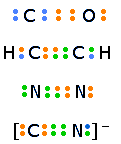
If one pair of electrons shared between two atoms constitutes a chemical bond, it seems logical that two or three pairs could be shared to produce double and triple bonds. Such formulations appear quite naturally when the octet rule is applied to elements such as C, O, S, and N.
The colors of the electron-dots in this illustration are intended only to help you keep track of the number of electrons contributed by each atom. Because electrons are indistinguishable, it makes no sense to identify a given electron-dot with a given atom.
Since multiple bonds place more electron density between the two nuclei, the latter are held toward each other more closely and tightly; multiple bonds are therefore shorter and stronger than single bonds.
Can there be bonds of higher order than three? No one thought so for a long time, but beginning in the 1960s, experiments and theoretical computations began to reveal that this just might be possible; some molecules just don't follow the rules!
bond type |
bonded atoms |
molecules |
when/who |
| quadruple | Re::::Re | [Re2Cl8]2– | 1964 F. Albert Cotton, Texas A&M University |
| quintuple | Cr:::::Cr | RCrCrR (R=large organic group) | 2005 Philip Power, U of California, Davis |
| sextuple | W::::::W | W2 | 2006 (Roos, Gagliardi, Borin, U of São Paulo) |
Adding to the fun, a 2006 article presented evidence that the carbon atom in C(PPh3)2 (where Ph stands for a benzene ring) has two lone pair electrons, but no electrons connected to the bonded groups— thus introducing the concept of a "zero-uple" bond.
Expanded octets
As mentioned previously, the octet rule works best for the elements in the second period (Li through F) of the periodic table. The reason for this is that electrons, whether shared or not, must be contained in orbitals, and the energies of electrons in such orbitals must be relatively low; otherwise, there would be no energetic advantage in forming a bond in the first place— the atoms would be better off by themselves.
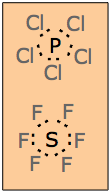 For the second- and third-period elements, the n=2 and n=3 s2p6 sets comprise the octet. Some of the third-period elements (Si, P, S, and Cl) can bond to more than four atoms, and thus need to involve more than the four pairs of electrons available in an s2p6 octet. This is possible because at n=3, an additional set of d orbitals can exist. Although their energies are higher (ordinarily higher than the 4s orbitals), they can participate in the valence shells of these atoms.
For the second- and third-period elements, the n=2 and n=3 s2p6 sets comprise the octet. Some of the third-period elements (Si, P, S, and Cl) can bond to more than four atoms, and thus need to involve more than the four pairs of electrons available in an s2p6 octet. This is possible because at n=3, an additional set of d orbitals can exist. Although their energies are higher (ordinarily higher than the 4s orbitals), they can participate in the valence shells of these atoms.
Examples of molecules in which the n=3 central atom contains an expanded octet are the phosphorus pentahalides and sulfur hexafluoride.
Similarly, for atoms in the fourth period and beyond, higher d orbitals can sometimes be used to accommodate additional shared pairs beyond the octet . If you review a diagram showing the relative energies of the different kinds of atomic orbitals (see here, for example), you will notice that all the energy gaps become smaller as the principal quantum number increases, so the energetic cost of using these higher orbitals becomes smaller.
Drawing a simple electron-dot structure
Drawing electron-dot structures is easiest if you follow the simple steps that are outlined below, using hydroxylamine, NH2OH, as an example.
1. Write out a simple structural diagram of the molecule in order to clearly show which atom is connected to which.
- If you are not sure of the bond connectivity, the structures of other similar molecules can often provide a useful clue. Thus if you know that ammonia, NH3, has nitrogen as its central atom, then you might recognize that hydroxylamine is just a derivative of ammonia in which one of the hydrogens has been replaced with a hydroxyl group:

- It's also useful to know that the atoms hydrogen, nitrogen and oxygen are commonly connected to 1, 3, and 2 other atoms, respectively.
- The simple molecules for which electron-dot structures are drawn can often be thought of as consisting of one or more "central" atoms to which other atoms are attached.
The points outlined above will become part of your "chemical intuition" as you develop more experience in writing out structures from molecular formulas.
2. Draw electron-dot structures of the individual atoms in the molecule.
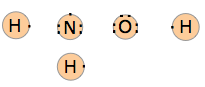
What you are doing here is showing how many valence electrons each atom contributes to the structure. We see that the total number of valence electrons is 14.
3. Bring the atoms together in a way that places eight electrons around each atom wherever possible.
Of the 14 valence electrons, 8 are needed to form the four covalent bonds in hydroxylamine, leaving six to be distributed as lone pairs. Placing these on the nitrogen and oxygen atoms as shown yields a structure conforming to the octet rule.
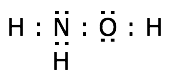
Electron-dot structures of ions
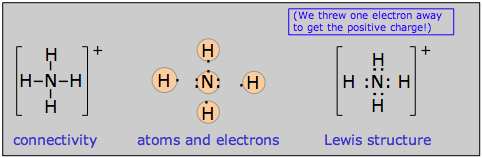
Ions are treated in basically the same way as neutral species, the only complication being that the number of electrons must be adjusted to account for the net electric charge of the ion. In other words, a negative ion contains more electrons than are provided by the valence shells of the constituent atoms, and a positive ion has fewer electrons than do the combining atoms. Here we show examples of the ammonium ion NH4+ which contains 9–1 = 8 electrons
... and of the chlorite ion ClO2–, which contains 19+1 = 20 electrons:

Electron-dot structures involving multiple bonds
The need for double or triple bonds usually becomes apparent when you have more electrons than can be accommodated in single bonds and lone pairs. Thus in the molecule acetylene (ethyne) C2H2, the single electrons contributed by the hydrogen atoms can be thought of as being paired up as one component of the carbon-carbon triple bond:

Multiple equivalent structures: resonance
There is a rather large class of molecules for which one has no difficulty writing Lewis structures; in fact, we can write more than one valid structure for a given molecule! Consider, for example, the nitrate ion NO3–. We can develop a Lewis dot formula satisfying the octet rule as follows:
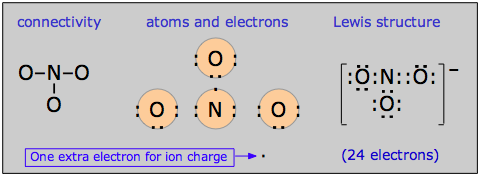
According to this structure, the ion contains two N–O single bonds and one N–O double bond. But there is no special reason to place the double bond where it is shown in the diagram above; it could equally well go in either of the other two locations. For this molecule, then, we can write three equally valid structures:
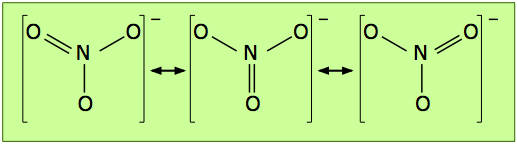
The double-ended arrows indicate that the nitrate ion is a superposition of all three structures, and this is supported by experimental evidence which shows that the three oxygen atoms are chemically identical, that all three bonds have the same length, and that the molecule has trigonal symmetry (meaning that the three oxygens are geometrically equivalent.)
The term resonance was employed to describe this phenomenon in the 1930's, before chemical bonding became better understood; the three equivalent structures shown above are known as resonance hybrids. The choice of the word "resonance" was unfortunate because it connotes the existence of some kind of dynamic effect that has led to the mistaken idea that the structure is continually alternating between the three possibilities.
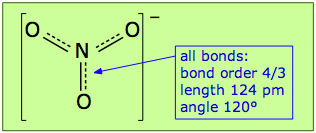 In actual fact, the nitrate ion has only one structure in which the electrons spread themselves evenly so as to make all three N–O links into "1-1/3 bonds"; we describe them as having a bond order of 4/3. The preferred way of depicting a molecule that has more than one equivalent bonding structure is to use dashed lines to indicate the "fractional" bonds as shown here.
In actual fact, the nitrate ion has only one structure in which the electrons spread themselves evenly so as to make all three N–O links into "1-1/3 bonds"; we describe them as having a bond order of 4/3. The preferred way of depicting a molecule that has more than one equivalent bonding structure is to use dashed lines to indicate the "fractional" bonds as shown here.
Very similar structures can be written for sulfur trioxide SO3, and for the carbonate ion CO32–.
In writing out resonance structures, it is important to bear in mind that only the electron pairs can be moved around; the atoms must retain the same connectivity. In some cases it is necessary to move electrons to locations that would produce a positive charge on one atom and a negative charge on the other. Since the separation of electric charge always costs energy, such resonance forms will tend to be less stabilizing and will not be as important contributors to the overall structure as those in where there is no charge separation.
Since electrons in molecules tend to arrange themselves into configurations that give the lowest possible energy, it is not surprising that the resonance hybrid represents a more stable (i.e., strongly bound) molecule than does any one of the contributing structures.
There is a good quantum-mechanical rationale for this; according to the Heisenberg uncertainty principle, the energy of the electron will be more uncertain as its position is more exactly specified. Since energies cannot be negative, the more “uncertain” the energy can be, the higher it can be. If an electron is spread out over two or three bonds in the hybrid instead of being confined to the space between only two atoms, its exact location is much less exactly known, and so its energy will be less uncertain, and therefore lower.
Resonance structures of carboxylic acids
This idea is embodied in the statement you will often see, particularly in the older literature, that a given structure “is stabilized by resonance”. This jargon has been used, for example, to explain the acidity of the -COOH group found in organic acids. Dissociation of a carboxylic acid such as formic acid yields a carboxylate ion –COO– which can be represented by two equivalent structures. These are more realistically interpreted as a single structure in which the C–O bond order is 1.5:
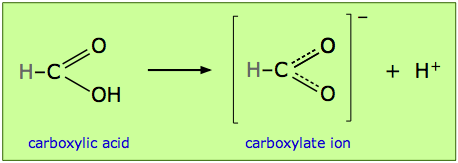
The idea is that resonance is only possible when the proton has been lost, and that the lower energy of the “resonating” structure provides the driving force for the loss of the proton, and thus is the source of the acidity carboxylic group. (By the way, this view of the cause of carboxylic acidity has been criticized; other factors that may well be more important are also involved.)
Resonance structures of the benzene ring
See here for a summary of the various structures that have been proposed for benzene over the years.
Perhaps the most well known molecule whose structure must be represented as a resonance hybrid is benzene, C6H6. The structure of this molecule had long been something of a mystery, in that it was difficult to understand how this formula could be consistent with the well-established tetravalence of carbon in organic compounds. The breakthrough came in 1865 when the German chemist August Kekulé proposed that the molecule is based on a hexagonal ring of carbon atoms as shown at the left below.
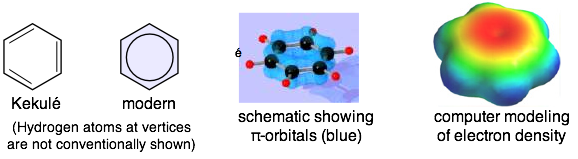
However, this structure is not consistent with the chemistry of benzene, which does not undergo the reactions that would be expected of a molecule containing carbon-carbon double bonds. Such compounds are normally quite reactive, while benzene, in contrast, tends to be rather inert to all but the most powerful reagents.
This apparent discrepancy disappeared after the resonance hybrid theory was developed; benzene is regarded as a hybrid of the two structures shown in the center above, and it is often depicted by the structure at the right, in which the circle represents a “half bond”, so that the bond order of each C–C bond is 1.5. Bond length measurements are entirely consistent with this interpretation; they are almost exactly halfway between the values found in compounds known to contain single and double bonds.
 A more realistic representation of the benzene molecule shows the two components of its bonds. The "sticks" joining adjacent carbons constitute "half" of the carbon-carbon bonding, while the circular charge clouds above and below the ring together make up the other "half". The details of this bonding arrangement are discussed in the section on the hybrid orbital model of bonding.
A more realistic representation of the benzene molecule shows the two components of its bonds. The "sticks" joining adjacent carbons constitute "half" of the carbon-carbon bonding, while the circular charge clouds above and below the ring together make up the other "half". The details of this bonding arrangement are discussed in the section on the hybrid orbital model of bonding.
Although there are many violations of the octet rule, most electron dot structures that one can write down in accordance with this rule and its general scope of validity correspond to molecules that actually exist. Sometimes, however, we are surprised to find that the molecules corresponding to an apparently reasonable Lewis formula are not known.
In some cases, this has been shown to be a consequence of the very high chemical reactivity of the molecules. Thus hypofluorous acid, HOF, has never been isolated, although its chlorine analog is well known. It was not until 1967 that its short-lived presence was detected spectroscopically. It is now believed that the molecule is stable, but that the products obtained when it reacts with itself are so much more stable that it decomposes almost as fast as it is formed:
2HOF(g) → 2HF(g) + O2(g)
Other molecules having proper Lewis structures but no apparent existence may be stable only at very low temperatures; examples are O4 and H2O4.
The fluorate ion, FO3–, has also never been detected, even though analogs containing the other halogen elements are well known. The problem here may well lie with the very small fluorine atom, which would allow the oxygens to approach so closely that they would repel each other.
Small size is also suggested as the reason for the non-existence of the nitrogen analogs of the sulfate and sulfite ions. These would have the formulas NO43– and NO32–. Here, the problem is believed to be the high charge density: it costs a lot of energy to squeeze this much electric charge in such a small volume. Sulfur, having a larger radius, forms larger ions having lower charge densities, and the total charge would also be only –2 instead of –3.
Molecules without proper Lewis electron structures
There are also examples of molecules whose existence is beyond question, but for which no satisfactory Lewis structures can be written. Two examples are the triiodide ion I3–, and the bifluoride ion HF2–.
The triiodide ion [I–I–I]– is a well known species found in aqueous solutions containing iodine and iodide ions:
I2 + I– → I3–
The bifluoride ion [F–H–F]– is formed in a rather similar way in hydrofluoric acid solutions containing fluoride ion:
HF + F– →HF2–
As you know, electrons tend to pair up in atoms and molecules so that their spins cancel out. If this does not happen— either because there is an uneven number of electrons or it is energetically unfavorable, then the species is said to be paramagnetic. Paramagnetic substances are attracted to a magnetic field, but unlike ferromagnetic materials such as iron, they do not retain their magnetic properties (act as magnets) in the absence of an applied field. Most molecules posses an even number of electrons and are diamagnetic.Try writing electron-dot structures for these two species, and you will see the problem!
Dioxygen
 The most abundant paramagnetic molecule in our world is the ordinary oxygen molecule which has twelve electrons. It is easy to write a proper Lewis structure for O2 that places an octet around each oxygen atom and a double bond between them. However, it takes only a simple experiment to show that the electrons in dioxygen cannot all be arranged in pairs: if you place a magnet near some liquid oxygen, the liquid will be drawn to the magnet. This can only mean one thing: there are at least two unpaired electrons in the O2 molecule. A more careful experiment shows that this number is exactly two. Are they in the bond or are they non-bonding electrons? You can decide this by sketching out a few possible structures.
The most abundant paramagnetic molecule in our world is the ordinary oxygen molecule which has twelve electrons. It is easy to write a proper Lewis structure for O2 that places an octet around each oxygen atom and a double bond between them. However, it takes only a simple experiment to show that the electrons in dioxygen cannot all be arranged in pairs: if you place a magnet near some liquid oxygen, the liquid will be drawn to the magnet. This can only mean one thing: there are at least two unpaired electrons in the O2 molecule. A more careful experiment shows that this number is exactly two. Are they in the bond or are they non-bonding electrons? You can decide this by sketching out a few possible structures.
The paramagnetism of oxygen is an anomaly in terms of the Lewis theory, although it is predicted by a more comprehensive theory that we will look at later. There are, however, a few other molecules that we would expect to be paramagnetic simply because they contain an odd number of valence electrons.
Nitric oxide and nitrogen dioxide
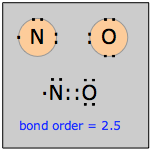 Nitrogen, having five valence electrons, forms two well-known odd-electron molecules with oxygen. Nitric oxide, NO, a colorless, odorless, paramagnetic gas, is the simplest stable odd-electron molecule known. It is clear that no structure conforming to the octet rule is possible. The Lewis structure shown here is somewhat misleading; chemical and physical evidence suggest that the unpaired electron is not localized on the nitrogen atom, but extends over the entire molecule.
Nitrogen, having five valence electrons, forms two well-known odd-electron molecules with oxygen. Nitric oxide, NO, a colorless, odorless, paramagnetic gas, is the simplest stable odd-electron molecule known. It is clear that no structure conforming to the octet rule is possible. The Lewis structure shown here is somewhat misleading; chemical and physical evidence suggest that the unpaired electron is not localized on the nitrogen atom, but extends over the entire molecule.
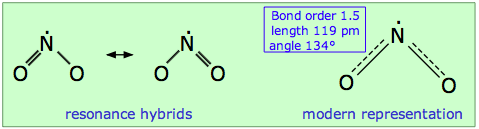
For example, if the structure were really ·NO, then we would expect the molecule to readily form a dimer ON:NO, but this is not observed. Bond-length measurements indicate that the N–O bond order is 2.5.
Nitric oxide has a remarkably rich chemistry. Until recently, its most famous role was as a precursor to photochemical smog. (The oxide is formed when fuels such as gasoline are burned at high temperatures in the presence of air.)
In the 1980s, to the surprise of almost everyone, NO was identified as an essential component of the signalling pathway of the mamallian cardiovascular system. As such, it provides a means by which cells communicate with one another. Other signalling molecules tend to be far more complicated, and no one would have expected a "free radical" molecule to have other than a damaging effect on the body. See here for a brief summary of some of the many roles nitric oxide plays in the body.
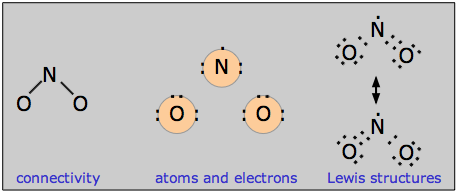
Nitrogen dioxide is also an odd-electron molecule. In contrast to NO, the odd electron in NO2 appears to be somewhat local to the nitrogen atom. As a consequence, the dimerization equilibrium
2 NO2 ![]() N2O4
N2O4
is so facile that neither gas can be retained in pure form at ordinary temperatures. Because two equivalent Lewis structures can be written, NO2 is a resonance hybrid in which the N–O bond order is 1.5.
More than one non-equivalent structure
It sometimes happens that the octet rule can be satisfied by arranging the electrons in different ways. For example, there are three different ways of writing valid electron dot structures for the thiocyanate ion SCN–. Some of these structures are more realistic than others; to decide among them, you need to know something about the concepts of formal charge and electronegativity. These topics are discussed in the lesson that follows this one, where examples of working out such structures are given.

 Irving Langmuir
Irving Langmuir

