Chem1 General Chemistry Virtual Textbook → acid-base equilibria 1
Fundamentals of proton-transfer reactions
Proton sources and sinks, proton free energy
On this page:
Acid-base reactions, in which protons are exchanged between donor molecules (acids) and acceptors (bases), form the basis of the most common kinds of equilibrium problems which you will encounter in almost any application of chemistry.
Important: In order to thoroughly understand the material in this unit, you are expected to be familiar with the following topics which were covered in the separate unit Introduction to Acid-Base Chemistry:
- The Arrhenius concept of acids and bases - Review now
- The Brønsted-Lowry concept, conjugate acids and bases - Review now
- Definition of pH and the pH scale - Review now
- Strong vs. weak acids and bases - Review now
You should also have some familiarity with the principles of chemical equilibrium, and know how to write and use equilibrium constants.
Proton transfer reactions
As you should recall from your earlier introduction to acids and bases, the +1 electric charge of the tiny proton (a bare hydrogen nucleus) is contained in such a miniscule volume of space that the resulting charge density is far too large to enable its independent existence in solution; it will always attach to, and essentially bury itself in, the non-bonding orbitals of a solvent. Thus in aqueous solution, what we commonly represent as the "hydrogen ion" H+ is more accurately described as the hydronium ion H3O+.
Acid-base chemistry is a transactional process in which protons are exchanged between two chemical species. A molecule or ion that loses or "donates" a proton is acting as an acid; a species that receives or "accepts" that proton plays the role of a base.
Defining an acid as a substance that simply "dissociates" into its component parts
HA → H+ + AB–
fails to capture the concept outlined in the above box. It is therefore important that you become comfortable with the Brønsted-Lowry model of acid-base behavior that represents the generalized acid-base reaction as a proton transfer process:

The actual electric charges of the reaction products will of course depend on the particular nature of the species A, but the base will always have one more negative charge than the acid HA.
Although anyone familiar with chemicals tends to regard certain substances as "acids" and others as "bases", it is important to bear in mind that these labels have meaning only in terms of the particular process being considered.
For example, in the absence of water, ammonia, which we usually think of as a base, can lose a proton (and thus act as an acid) to a "stronger" base B to form the amide ion:
NH3 + B → NH2– + HB+
Similarly, anhydrous sulfuric acid can accept a proton from a stronger acid AH:
H2SO4 + AH → H3SO4+ + A–
... but this is rather exotic stuff that is beyond the scope of this introductory lesson.
The acid-base processes we describe in this set of lessons take place in aqueous solution, so we will always assume that H2O, which can act either as a proton donor or proton acceptor, plays an active role.
Thus a substance that acts as an acid in aqueous solution donates a proton to H2O, yielding the hydronium ion H3O+.
HA + H2O → H3O+ + A–
Similarly, a base will remove a proton from H2O, yielding the hydroxide ion OH–.
B + H2O → BH+ + OH–
Autoprotolysis
A small number of acids are themselves amphiprotic, meaning that one molecule can transfer a proton to another molecule of the same kind. The best-known example of this process, known as autoprotolysis, is of course that of water:
2 H2O(l) → OH– + H3O+(1-1)
Pure liquid ammonia and sulfuric acid are other well-known examples:
2 NH3(l) → NH2– + NH4+
2 H2SO4(l) → HSO4– + H3SO4+
Autoprotolysis reactions such as these typically proceed to only a very small extent.
The ion product of water
The equilibrium constant for Eq 1 is commonly written as
Kw = [H+][OH–] (1-2)
For more on Kw, see this Wikipedia article, or this somewhat more detailed LSBU (UK) page.
and is usually known as the dissociation constant or ion product of water. For most purposes in elementary courses, we can use the value 1.0 × 10–14 for Kw. But you should understand that this value is correct only for pure water at 25° C and 1 atm pressure. Kw varies considerably with temperature, pressure, and the ionic content of water:
It should be obvious that anyone working in the fields of physiological or oceanographic chemistry cannot routinely use 1.0 × 10–14 for Kw!
The equilibrium constants Ka and Kb
Acids and bases vary greatly in their "strength" — that is, their tendencies to donate or accept protons.
As with any chemical reaction, we can define an equilibrium constant Kc whose numerical value reflects the extent of the reaction — that is, the relative concentrations of the products and reactants when the reaction reaches equilibrium.
The strength of an acid HA in water can be defined by the equilibrium
| HA + H2O → H3O+ + A– | 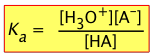 |
(1-3a) |
Similarly, the strength of the base A− in water is defined by
| A− + H2O → HA + OH– |  |
(1-3b) |
Note carefully that reaction (3a) is not the reverse of (3b)!
Ka and Kb are inversely proportional
How are Ka and Kb related? The answer can found by multiplying the above two expressions for Ka and Kb:
 (1-3)
(1-3)
Alternatively, we can simply add the two corresponding reaction equations:
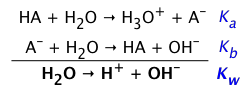
and — as you should recall from your earlier study of equilibrium, the equilibrium constant of the sum of two reactions is the product of the two K's. So either way you figure it, the Ka for an acid and Kb for its conjugate base are related in a very simple way:
Ka Kb = Kw (1-4)
Clearly, as the strength of a series of acids increases, the strengths of their conjugate bases will decrease, this inverse relation between Ka and Kb is implicit in Eq 4.
You will recall that the pH scale serves as a convenient means of compressing a wide range of [H+]-values into a small range of numbers. Just as we defined the pH as the negative logarithm of the hydrogen ion concentration, we can define
pK = − log K(2-5)
for any equilibrium constant. Acid and base strengths are very frequently expressed in terms of pKa and pKb.
From Eq 4, it should be apparent that
pKa + pKb = pKw (= 14.0 at 25◦ C)(1-5)
pK values of some common acids and bases
In order to convert pKa into Ka, simply take the negative antilog of pKa. Thus, for acetic acid with
pKa = 4.7, Ka = 10–4.7 = 2.0E–5.
The following table gives the pKa values for a number of commonly-encountered acid-base systems which are listed in order of decreasing acid strength. It's worth taking some time to study this table in some detail.
Please take special note of the following points:
- Acids (1-4) are the major strong acids. All dissociate in water to produce the hydronium ion (5), the strongest acid that can exist in water.
- (6) H2SO3 has never been detected; "sulfurous acid" and its formula refer to a solution of SO2 in water.
- The names bisulfate (3, 7), bisulfite (6, 16), and bicarbonate (13) are still commonly used by chemists, but the preferred names are now hydrogen sulfate, hydrogen sulfite, and hydrogen carbonate, respectively. Similarly, bisulfide (14, 26) is also known as hydrosulfide.
- The ion (9) as it exists in aqueous solution is often represented as Fe3+ and is known more commonly as the ferrous or iron(III) ion. The aqueous aluminum ion Al3+ (12) as well as many transition metal ions have similarly complex structures and give acidic solutions in water because the high positive charge increases the acidity of the attached H2O units. For more on these aquo complexes, see this brief discussion, or this much more detailed one by Jim Cook of the UK.
- The molecule H2CO3 (13) exists as a minority species in an aqueous solution of CO2 and has never been isolated. In most contexts, the formula H2CO3, the name carbonic acid and the pKa 6.3 refer to "total dissolved CO2" in the water. "True" H2CO3 is about a thousand times stronger than the pKa of its equilibrium mixture with CO2(aq).
- The sulfide, amide and oxide ions (26-28), being stronger bases than OH–, cannot exist in water.
| ref | acid | pKa | conjugate base | pKb | |
|---|---|---|---|---|---|
| 1 | HClO4 | perchloric acid | ~ –7 | ClO4– chlorate | ~ 21 |
| 2 | HCl | hydrochloric acid | ~ –3 | Cl – chloride | ~ 17 |
| 3 | H2SO4 | sulfuric acid | ~ –3 | HSO4– bisulfate | ~ 17 |
| 4 | HNO3 | nitric acid | ~ –1 | NO3– nitrate | 15 |
| 5 | H3O+ | hydronium ion | 0 | H2O water | 14.00 |
| 6 | H2SO3 | sulfurous acid | 1.8 | HSO3– bisulfite | 12.2 |
| 7 | HSO4– | bisulfate ion | 1.9 | SO42– sulfate | 12.1 |
| 8 | H3PO4 | phosphoric acid | 2.12 | H2PO4– dihydrogen phosphate | 11.88 |
| 9 | [Fe(H2O)6]3+ | hexaaquoiron(III) | 2.10 | [Fe(H2O)5OH]2+ | 11.90 |
| 10 | HF | hydrofluoric acid | 3.2 | F – fluoride | 10.8 |
| 11 | CH3COOH | acetic acid | 4.76 | CH3COO – acetate | 9.3 |
| 12 | [Al(H2O)6]3+ | hexaaquoaluminum(III) | 4.9 | [Al(H2O)5OH]2+ | 9.1 |
| 13 | H2CO3 | carbonic acid | 6.3 | HCO3– bicarbonate | 7.7 |
| 14 | H2S | hydrogen sulfide | 7.04 | HS –bisulfide | 6.96 |
| 15 | H2PO4– | dihydrogen phosphate | 7.2 | HPO4– monohydrogen phosphate | 6.8 |
| 16 | HSO3– | bisulfite ion | 7.21 | SO32– sulfite | 6.79 |
| 17 | HOCl | hypochlorous acid | 8.0 | OCl – hypochlorite | 6.0 |
| 18 | HCN | hydrocyanic acid | 9.2 | CN – cyanide | 4.8 |
| 19 | H3BO4 | boric acid | 9.30 | B(OH)4– borate | 4.79 |
| 20 | NH4+ | ammonium ion | 9.25 | NH3 ammonia | 4.75 |
| 21 | Si(OH)4 | ortho-silicic acid | 9.50 | SiO(OH)3– silicate | 4.50 |
| 22 | HCO3– | bicarbonate ion | 10.33 | CO32– carbonate | 3.67 |
| 23 | HPO42– | monohydrogen phosphate ion | 12.32 | PO43– phosphate | 1.67 |
| 24 | SiO(OH)3– | silicate ion | 12.6 | SiO2(OH)22– | 1.4 |
| 25 | H2O | water | 14.00 | OH – hydroxide | 0 |
| 26 | HS – | bisulfide ion | ~ 19 | S 2– sulfide | ~ –5 |
| 27 | NH3 | ammonia | ~ 23 | NH2 – amide | ~ -9 |
| 28 | OH – | hydroxide ion | ~ 24 | O 2– oxide | ~ –10 |
The concept of the "potential energy of the proton" (more properly, proton free energy), is not nearly as intimidating as it might sound; it is easy to grasp, requires no mathematics, and will enable you to achieve a far better understanding of acid-base chemistry.
Most courses (and their textbooks) do a good job of explaining the concept of proton transfer, but few of them provide you with a clear basis for understanding and making useful predictions about the direction and extent this transfer will take. For example, when the gas HCl is added to water, you probably know that the reaction proceeds strongly to the right:
HCl + H2O → H3O+ + Cl– (2-1)
...but what principle determines this, and what is to prevent the hydronium ion (also an acid) from pushing one of its own protons back onto a chloride ion, and thus reversing the reaction?
The concept of the proton free energy level was introduced in R.W. Gurney's classic Ionic Processes in Solution (1953). The best detailed exposition can be found in the first (1970) edition of Aquatic Chemistry by W. Stumm and J.L. Morgan.
The answer is that a proton is never really "pushed"; it will spontaneously seek out the lowest potential energy state (that is, the strongest base) it can find. Think how a macroscopic object such as a book will tend to fall to a location where its [gravitational] potential energy is as low as possible. Of course, the potential energy of a proton has nothing to do with gravity, but rather with how tightly it can bind to a base. This kind of potential energy is known as proton free energy (PFE) — but in the context of first-year chemistry, we can also just call it "proton energy".
You are not sure what free energy is? Don’t worry about it for the time being; just think of it as you would any other form of potential energy: something that falls when chemical reactions take place. See here for the lesson on free energy.
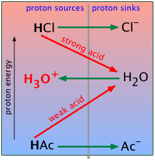
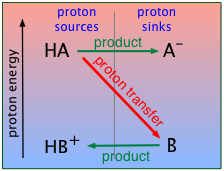 For the present, all you need to know is that a proton will tend to "fall" to the lowest potential energy state it can find. In keeping with this idea, you can think of an acid as a proton source, and a base as a proton sink. Using this terminology, we can depict the generalized process HA + B → AB– + HB+ as in this plot, which depicts the proton on HA "falling" to the lower-PFE "sink" provided by the base B, leaving AB– and HB+ as products.
For the present, all you need to know is that a proton will tend to "fall" to the lowest potential energy state it can find. In keeping with this idea, you can think of an acid as a proton source, and a base as a proton sink. Using this terminology, we can depict the generalized process HA + B → AB– + HB+ as in this plot, which depicts the proton on HA "falling" to the lower-PFE "sink" provided by the base B, leaving AB– and HB+ as products.
We will be making a lot of use of schematics like this farther on, so take a moment to familiarize yourself with information it depicts.
This "source/sink" nomenclature recalls the tendency of water to flow down from a high elevation to a lower one; this tendency (which is related to the amount of energy that can be extracted in the form of electrical work if the water flows through a power station at the bottom of the dam) will be directly proportional to the difference in elevation (difference in potential energy) between the source (top of the dam) and the sink (bottom of the dam).
Thus you can regard proton free energy as entirely analogous to the gravitational potential energy of the water contained in a dam; in this case, we are dealing with chemical potential energy, more commonly known as free energy.
Take particular note of the following:
- The ordinate represents the relative free energy of a mole of protons when attached to a given base; we label it simply "proton energy" for brevity.
- The gray vertical line at the center of the diagram separates the acidic form of each conjugate pair from its base form; the terms "proton sources" and "proton sinks" are there to remind us of the role these forms play in acid-base chemistry.
- The red diagonal arrow represents the actual process in which a mole of protons "falls" from the acid HA to the base B. The fact that the arrow slants downward indicates that this process is spontaneous, meaning that the reaction proceeds to completion. In other words, the equilibrium constant for this reaction is very large.
- The green horizontal arrows depict the changes (that is, the formation of the two new conjugate species) that result from the proton transfer as the protons "fall" (in free energy) from the acid HA to the base B.
Strong acids in water
When you were first introduced to the Brønsted-Lowry model, you learned that the proper way to represent the "dissociation" of a strong acid like hydrochloric is
HCl + H2O → H3O+ + Cl– (2-1)
Thus water is revealed as an active participant in the behavior of an acid, rather than as an inert spectator or solvent. Although analogous acid-base reactions can take place in other solvents such as liquid ammonia, virtually all of the acid-base chemistry we encounter in daily life is based on water.
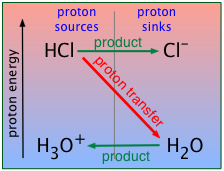 Since water is acting as the proton acceptor here, it must be fulfilling the role of the base B in the schematic given above. We can therefore construct a similar plot specifically for HCl (or, in fact, for any strong acid).
Since water is acting as the proton acceptor here, it must be fulfilling the role of the base B in the schematic given above. We can therefore construct a similar plot specifically for HCl (or, in fact, for any strong acid).
Recall that, for strong acids, this reaction is essentially complete. This means that a "solution of hydrochloric acid" is in reality a solution of hydronium and chloride ions; except in solutions much more concentrated than 1 M, the species HCl is only present in trace amounts.
Weak acids in water
When acetic acid CH3COOH is dissolved in water, the resulting solution displays only very mild acidic properties. For simplicity we will represent acetic acid and the acetate ion CH3COO– by HAc and Ac–, respectively:
HAc + H2O → H3O+ + Ac– (2-2)
But although this equation has the same form as (2-1) above, it hides an important qualitative difference: HAc is a weak acid, meaning that the proton transfer takes place to only a tiny extent; the equilibrium strongly favors the left side:
HAc + H2O ![]() H3O+ + Ac–
H3O+ + Ac–
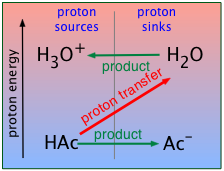 The corresponding proton free energy diagram now shows the H3O+-H2O system at the top, with the proton-transfer arrow pointing upward, indicating that the protons get kicked up to a higher free-energy level in this process.
The corresponding proton free energy diagram now shows the H3O+-H2O system at the top, with the proton-transfer arrow pointing upward, indicating that the protons get kicked up to a higher free-energy level in this process.
Where does this additional energy come from? Simply from the random thermal energy in the solution. As you might expect, this is not a thermodynamically favorable process, so it only happens to a very small extent. In contrast to the HCl example we described previously in which 99.99+ percent of the HCl molecules end up as hydronium ions, almost all of the acetic acid molecules remain unchanged, and only tiny amounts of H3O+ and Ac– are produced.
Strong and weak acids both donate protons to water, yielding hydrogen ions and thus rendering the solution acidic.
What's different is that virtually all of the protons of the strong acid "fall" to the H2O level, whereas only a tiny fraction of the weak acid molecules acquire enough thermal energy to promote their protons up to the H2O level.
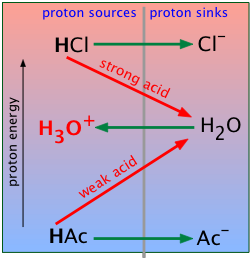 The fundamental difference between strong acids and weak acids is clearly evident when we combine the preceding two proton-free energy diagrams into one. Strong acids (strong "conjugate-pairs") are always above the PFE of the H3O+-H2O system, while the weak conjugate pairs are below it.
The fundamental difference between strong acids and weak acids is clearly evident when we combine the preceding two proton-free energy diagrams into one. Strong acids (strong "conjugate-pairs") are always above the PFE of the H3O+-H2O system, while the weak conjugate pairs are below it.
The other big difference with acetic acid is that water is acting as a base here, rather than as an acid as it did in the HCl example. So it's not surprising that water, the basis of almost all acid-base chemistry, should appear in the middle of these diagrams.
Water can swing both ways
Substances that can both donate and accept protons are said to be amphiprotic. Many oxides and hydroxides behave in this way, and since H2O falls into both of these classes, it is not surprising that water is amphiprotic:
Water-the-acid: H2O + B → BH+ + OH–
Water-the base: H2O + AH → H3O+ + A–
("AH" above represents any acid; B stands for any base)
These two opposing tendencies can be represented by

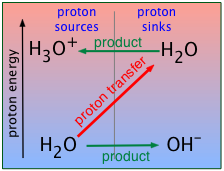 In the case of water, the contest is a draw; not only does neither side win, but the fraction of
In the case of water, the contest is a draw; not only does neither side win, but the fraction of
H2O molecules that break up in this way is miniscule: In pure water, only about one H2O molecule out of 109 is “dissociated” at any instant:
H2O ![]() H+ + OH– (2-4)
H+ + OH– (2-4)
The actual reaction, of course, is the proton transfer
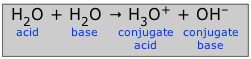 (2-5)
(2-5)
for which the equilibrium constant
Kw = [H3O+][OH–] (2-6)
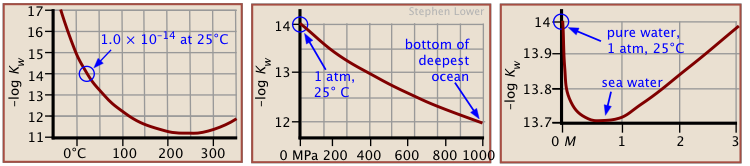
is known as the ion product of water. The value of Kw at room temperature is 1.008 x 10–14. We can also express this in logarithmic terms: pKw = 14.0.
As with any equilibrium constant, the value of Kw is affected by the
- temperature: Kw undergoes a 10-fold increase between 0°C and 60°C
- pressure: Kw is about doubled at 1000 atm
- presence of ionic species in the solution.
Because most practical calculations involving Kw refer to ionic solutions rather than to pure water, the common practice of using 10–14 as if it were
a universal constant is unwise; under the conditions commonly encountered in the laboratory, pKw
can vary from about 11 to almost 15. In seawater,
Kw is 6.3 × 10−12. (See Stephen J. Hawkes: “pKw is almost never 14.0”, J. Chem. Education 1995: 72(9) 799-802)
Notice that under conditions when Kw differs significantly from
1.0 × 10–14, the pH of a neutral solution will not be 7.0.
For example, at a pressure of 93 kbar and 527°C, Kw = 10−3.05, the pH of pure water would be 1.5. Similarly unusual conditions apply to deposits of water in geological formations and in undersea vents.
At 60° C, the ion product of water is 9.6E–14. What is the pH of a neutral solution at this temperature?
Solution: Under these conditions, [H+][OH–] = 9.6E–14. If the solution is neutral,
[H+] = [OH–] = (9.6E–14)½ = 3.1E–7, corresponding to a pH of
log 3.1E-7 = 6.5.
The leveling effect
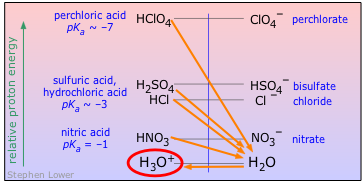 The strengths of strong acids and bases are "leveled" in water. This means that all strong acids and strong bases are equally strong in water. To see this more clearly, notice that the free energies of protons in all of these acids (even nitric) are sufficiently above the H3O+/H2O level that their "dissociation" is essentially complete. Thus
The strengths of strong acids and bases are "leveled" in water. This means that all strong acids and strong bases are equally strong in water. To see this more clearly, notice that the free energies of protons in all of these acids (even nitric) are sufficiently above the H3O+/H2O level that their "dissociation" is essentially complete. Thus
The strongest acid that can exist in water is H3O+ ;
The strongest base that can exist in water is OH–
Similarly, the hydroxide ion is the strongest base that can exist in water.
So what happens if you add a soluble oxide such as Na2O to water? Since O2– is a proton sink to H2O, it will react with the solvent, leaving OH– as the strongest base present:
Na2O + H2O → 2 OH– + Na+ .
Thus all bases stronger than OH– appear equally strong in water — simply because they are all converted to OH– .
PFE's are the key to understanding acid-base reactions
In the preceding section, we have employed simple PFE (proton free energy) diagrams to help you better understand the concepts of strong and weak acids, water as an acid or a base, and the leveling effect.
But we can gain a more generalized and comprehensive view of acid-base chemistry with the aid of a PFE diagram that shows a whole series of acid-base systems, arranged in order of decreasing acid strengths.
How acid strengths relate to proton free energies
As we explained near the beginning of this lesson, we ordinarily express the strength of an acid by quoting its "dissociation constant" Ka, which is the equilibrium constant for transfer of a proton to the base H2O.
HA + H2O → H3O+ + A–
We also introduced the concept of PFE as an alternative way of expressing the strength of an acid. If both PFE and Ka express the same thing, you may wonder how these two quantities are related.
If you have had an introduction to thermodynamics and specifically to free energy G, you might wish to look at the Appendix section of this lesson to review the relationship between the fall in free energy and the value of pKa.
A thorough answer to this question requires a bit of thermodynamics, which you may not have yet studied, but you don't really need any of the math here. It should suffice to show the results in the form of a plot, which yields a simple straight-line relationship when plotted on a semi-logarithmic scale.
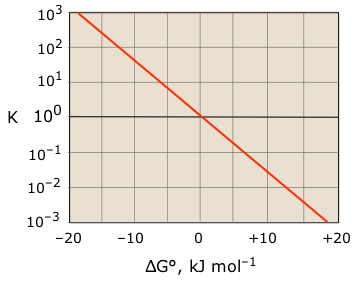 Note that
Note that
- The extent of any chemical reaction is proportional to the fall in free energy when it takes place. So negative ΔG values correspond to larger equilibrium constants.
- For acid-base reactions specifically, Ka is inversely proportional to ΔG, and thus to the fall in PFE.
- This means that the proton on a strong acid (Ka > 1) has a large negative PFE; it has a "long way to fall" to the H2O level.
- Conversely, a proton on a weak acid (Ka <1) can only move up to the H2O level when supplied with thermal energy from the surroundings.
- A K value of 100 = 1 corresponds to a zero-free energy change, meaning that the reaction is at equilibrum when [HA] = [A–].
- Proton-free energy changes exceeding –20 kJ mol–1 result in Ka values so large that the proton transfer can be considered "complete" for most practical purposes.
Understanding the PFE chart
On the PFE diagram shown below, each acid-base system is represented by a horizontal line connecting an acidic species with its conjugate base. Each line is placed at a height on the diagram that is proportional to its pKa, as measured on the logarithmic scale (labeled "pH") at the right. What we have, then, is a list of acid-base systems arranged in order of decreasing acid strength.
Think of this chart as an alternative view of the table of acid strengths displayed near the top of this page, in which some of the information that is "hidden" in the table is now revealed in an easily-grasped way.
Take particular note of the following points:
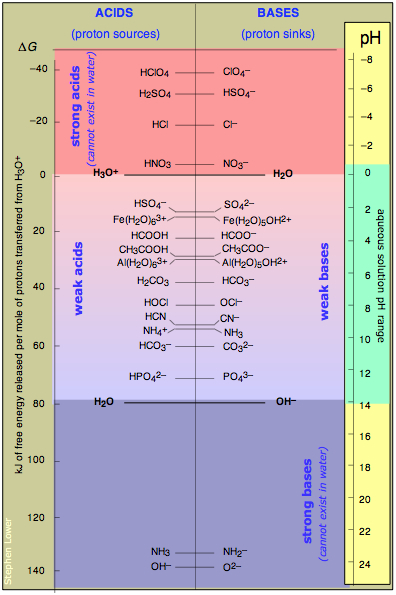
- The ΔG scale on the left measures the fall in potential energy when one mole of protons is transferred from a given acid to H2O. Negative values correspond to stronger acids.
- Any acid shown on the left side of the vertical line running down the center of the diagram can donate protons to any base (on the right side of the line) that appears below it.
The value of the equilibrium constant for such a reaction will exceed unity; for ΔG separations of more than about 10 kJ/mol, the reaction can be considered to be complete. - The zero free energy assigned to the hydronium ion corresponds to the standard free energy of formation ΔGf° of this ion.
- Notice how the two conjugate pairs H3O+ / H2O and H2O/OH– bracket the 80-kJ/mol region that comprises the weak acids. The weakness of these acids reflects the energetic cost of moving a proton "up-hill" to the H2O level.
- The strong acids at the top of the table can all be regarded as totally "dissociated" in water. This means that these acids cannot exist in water, as they are totally transformed into H3O+. Of course, they will also react with any bases below the H2O level that may be available. (See "leveling effect" below.)
- Similarly, the two strong bases NH2– and O2– shown at the bottom of the table cannot exist in water. Thus if solid sodium oxide Na2O is added to water, the oxide ions are such a low-energy sink that will totally fill up with protons from the H2O acid level which defines the top of the strong-base range.
- Notice the pH scale along the right side, and note the range of pH values possible in water. We will say more about the significance of pH in these diagrams farther on.
The PFE chart helps you visualize (and understand!) acid-base chemistry
The virtue of a PFE chart is that you can see, at a glance, the relations between conjugate acid-base pairs that enables you to make quick, qualitative determinations of what is going on even in complex mixtures of acids and bases. The speed and convenience this affords enables you to build a much deeper conceptual understanding of acid-base chemistry.
In order to do the same thing by consulting a simple list of acid Ka's or pKa's, you also need to be familiar with the principles of chemical equilibrium and thermodynamics — and then take the time to work through the arithmetic.
In the preceding sections we have shown how the PFE-chart approach can clarify the distinction between strong and weak acids. We will now go on to describe a variety of other principles that are easily grasped by consulting a PFE chart.
Significance of the pH scale
You will have noticed the scale labeled "pH" at the left side of the PFE plot.
First, please understand what this scale does NOT do; it does not tell you what the pH of the solution will be when you add an acid to pure water. This pH will depend on both the strength (Ka or pKa) of the acid, and on its concentration in the resulting solution; you will learn how to carry out pH calculations in later lessons.
All but the very weakest acids can drive the pH down to near the bottom of the scale if their solutions are sufficiently concentrated. The only thing you can be sure of is that the pH of a solution of a solution of an acid in pure water will never be greater than 7.
pH sets the average proton free energy
When pH was first introduced in 1909, it was defined in terms of the "hydrogen ion concentration" [H+]. This has since been amended to the hydrogen ion activity {H+}. The latter term refers to the "effective" concentration of these ions — that is to the "availability" of protons (regardless of whether they physically exist as H3O+ units or in other forms) to react with bases. But from the standpoint of thermodynamics, "availability" is just a loose term for "free energy". So we can also say that
pH is a measure of the average PFE in an aqueous solution
The more negative the pH, the higher the proton free energy in the solution. (The inverse relation is a consequence of the negative-logarithm definition of pH.)
The pH has the dual advantages of being both dimensionless and readily observable. More importantly, we can easily alter the pH of a solution by adding some strong acid or base. And when we do this, we are in effect using the pH as a tool for controlling the average PFE in the solution.
More on this in a moment; first, let us introduce an important relation that you may have seen in an earlier chemistry course, and which we will discuss more in a later lesson in this group.
pH can control the relative abundance of conjugate acid-base pairs
Recalling the equilibrium expression for a weak acid
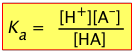 (3-1)
(3-1)
We can solve this for [H+]:
![]() (3-2)
(3-2)
Re-writing this in terms of negative logarithms, this becomes
![]() (3-3)
(3-3)
or, since pKa = – log Ka, we invert the ratio to preserve the positive sign:
We will make extensive use of this equation in a later lesson on acid-base buffering and titration.
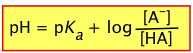 (3-4)
(3-4)
This extremely important relation tells us that the pH of a solution containing a weak acid-base system controls the relative concentrations of the acid and base forms of that system.
Of special interest is the case in which the pH of a solution of an acid-base system is set to the value of its pKa. According to the above equation, when pH = pKa, the log term becomes zero, so that the ratio
[AB–] / [HA] = 100 = 1, meaning that [HA] = [AB–]. In other words,
This pH adjustment can be easily made by adding appropriate amounts of a strong acid or strong base to the solution.
When the pH of a solution is set to the value of the pKa of an acid-base pair, the concentrations of the acid- and base forms will be identical.
This condition can be represented schematically:

This is the basis for the arrangement of the various acid-base systems depicted in the PFE diagram; each conjugate pair is placed at a location on the vertical pH scale that corresponds to the acid's pKa.
It is instructive to consider how sensitively the concentration ratio [A–] / [HA] depends on the pH.
Hypochlorous acid, HOCl, has a pKa of 8.0.
a) Estimate the ratio R = [OCl–] / [HOCl] in a solution of sodium hypochlorite whose pH has been adjusted to 8.2.
b) If the initial concentration of the hypochlorite solution was 0.10M, what will be the concentrations of the acid and base forms at pH 8.2?
Solution:
a) Substituting in Eq 3-4, the log term becomes (8.2 – 8.0) = 0.2,
so R = 100.2 = 1.6.
Note that it does not matter whether the initial solution consists of HOCl or NaOCl or some mixture thereof; adjusting the pH forces the system composition to the ratio calculated above.)
b) In the resulting solution, the base form OCl– is the predominant species, the mole ratio R being 1.6/1. The mole fraction of OCl– will therefore be 1.6/2.6 = 0.62, making that of HOCl (1.0 – .62) = 0.38. The actual concentrations will be 0.1 times these values, reflecting the 0.10M concentration of the solution.
To what pH must we adjust a solution of acetic acid (pKa 4.7) in order to convert 20 percent of the acid into its base form?
Solution: In the final solution, the mole fractions will be [AB–] = .20, [HA] = 0.80; the ratio [AB–]/[HA] = .20/.80 = 0.25. Substituting into Eq 2-9, we have
pH = 4.7 + log .25 = 4.7 – 0.6 = 4.1
We can explore the relation between the pH and the distribution of conjugate species between the acid and base forms by carrying out calculations similar to those in Problem Example 2 for an acid-base system at different pH values.
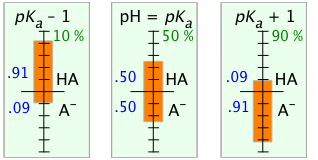 The orange bars and blue numbers show the mole fractions of the acid and base forms at pH values of the pKa and the pKa ± 1. The green numbers give the percent dissociation of the acid at each pH.
The orange bars and blue numbers show the mole fractions of the acid and base forms at pH values of the pKa and the pKa ± 1. The green numbers give the percent dissociation of the acid at each pH.
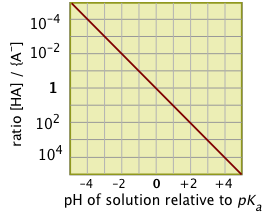 The apparent symmetry between the two extreme pH values suggests a simple relation between the log of the ratio
The apparent symmetry between the two extreme pH values suggests a simple relation between the log of the ratio
[AB–] / [HA] and the pH. This is seen very clearly when this ratio is plotted as a function of pH.
 Solutions containing many different weak acid-base systems are very commonly encountered in nature, especially in biological fluids or natural waters, including the ocean. When the pH of such solutions is altered by the addition of strong acid or base (as can occur, for example, when wastes from industrial processes or mine drainage, or acidic rain, enter a lake or stream); the distribution of all conjugate acid-base systems will change.
Solutions containing many different weak acid-base systems are very commonly encountered in nature, especially in biological fluids or natural waters, including the ocean. When the pH of such solutions is altered by the addition of strong acid or base (as can occur, for example, when wastes from industrial processes or mine drainage, or acidic rain, enter a lake or stream); the distribution of all conjugate acid-base systems will change.
It is important to note that the [AB–] / [HA] ratios (calculated here from Eq 3-4) yield only a qualitative picture and do not take into account the concentrations of the different acid-base systems or proton transfers between them. The latter processes would cause the lowest proton-vacant levels (that is, the strongest bases) to be completely filled from the bottom up, depending on the number of protons available. An exact calculation would require solving a set of simultaneous equations and is beyond the scope of this lesson.
Make sure you thoroughly understand the following essential concepts that have been presented above.
- Write a chemical equation for the autoprotolysis of a species such as HCO3–; write an equation for the equilibrium constant for this reaction.
- Write equations that express the chemical reactions and equilibrium constant expressions that define the strength of an acid or base in terms of proton transfer processes (Brønsted-Lowry concept).
- Write expressions defining the equilibrium constants Ka and Kb.
- Given the value of any two of Ka, Kb, and Kw, evaluate the third one. (This requires that you can show that Ka × Kb = Kw.)
- Explain the significance of the value of pKa for a given monoprotic acid-base system — that is, what it tells us about that particular acid and its conjugate base.
- Sketch out a simple proton free energy (PFE) diagrams illustrating the distinction between monoprotic strong and weak acids.
- State the meaning of the leveling effect, and construct a simple PFE diagram that illustrates its action.
- Describe, in your own words, the meaning of PFE, how it relates to pH, and in its significance in terms of the relative concentrations of a conjugate acid-base pair in a solution.
A. What do we mean by the "strength" of an acid ?
The Brønsted-Lowry model defines the strength of an acid HA as its tendency to donate protons to a base B. But bases vary in their abilities to accept protons, so the tendency for the complete transaction
HA + B → BH+ + A–(A-1)
to occur depends on the two processes
HA → H+ + A– K1 (A-2)
B + H+ → BH+ K2(A-3)
Ka's are always expressed on a scale relative to the Kb of the solvent
Because it is impossible to study either of these steps independently, what we might call the "absolute" strength of an acid (Eq A-2) cannot be measured. For this reason, we define a "standard" base, usually the solvent, and most commonly, water. Thus we replace Eq A-3 with
H2O + H+ → H3O+K3(A-4)
so that Eq A–1 now expresses the strength of HA relative to the base H2O:
HA + H2O → H3O+ + A– (A-5)
which, for convenience, we write in its abbreviated form
HA → H+ + A– (A-5)
whose equilibrium constant is
 (A-6)
(A-6)
B. pH and proton free energy
This section may be of interest to readers who have studied elementary thermodynamics, and have some familiarity with Gibbs free energy. it is not required for understanding and using the concept of PFE.
From elementary thermodynamics, the driving force of a chemical reaction is given by the standard free energy change:
ΔG° = –RT ln K (B-1)
Solving this equation for K yields
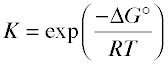 (B-2)
(B-2)
For a weak acid we know that
![]() (B-3)
(B-3)
Substituting Eq B-2 into this expression, we get
![]() (B-4)
(B-4)
Next, we take the negative log of each term, recalling that ln x = 2.3 log x:
![]() (B-5)
(B-5)
or
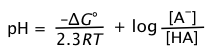 (B-6)
(B-6)
For the special case in which the concentrations of the conjugate pairs [H+] and [HA] are equal, pH = pKa, and the rightmost term above disappears, leaving
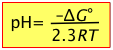 (B-7)
(B-7)
Thus the pH is a direct measure of the average proton free energy in a solution.
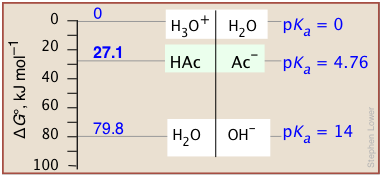
Construct a PFE diagram showing a) H3O+, b) acetic acid HAc (pKa = 4.76),
and c) H2O.
Solution: Solving Eq A–13 for ΔG° yields ΔG° = (2.3RT) × pKa, or, at 25°C,
ΔG° = (2.3 × 8.314 J K–1 mol–1) × pKa = 5698 J K–1 mol–1 × pKa
a) The proton in H3O+ is already at the level of that in the standard base H2O
(Eq A–5), so for this transfer is [by definition] ΔG° = 5698 J K–1 mol–1 × 0 = 0
b) The increase in the free energy required to transfer a proton from its level in HAc to that in H2O is ΔG° = 5698 J K–1 mol–1 × 4.76 = 27.1 kJ mol–1
c) To transfer a proton from H2O to another H2O (autoprotolysis), its free energy must increase by 5698 J K–1 mol–1 × 14.0 = 79.8 kJ mol–1