Semipermeable membranes and osmotic flow
Osmosis is the process in which a liquid passes through a membrane whose pores permit the passage of solvent molecules but are too small for the larger solute molecules to pass through.
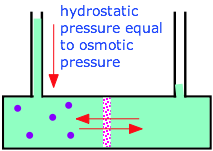 The figure shows a simple osmotic cell. Both compartments contain water, but the one on the left also contains a solute whose molecules (represented by blue circles) are too large to pass through the membrane. Many artificial and natural substances are capable of acting as semi-permeable membranes. The walls of most plant and animal cells fall into this category.
The figure shows a simple osmotic cell. Both compartments contain water, but the one on the left also contains a solute whose molecules (represented by blue circles) are too large to pass through the membrane. Many artificial and natural substances are capable of acting as semi-permeable membranes. The walls of most plant and animal cells fall into this category.
If the cell is set up so that the liquid level is initially the same in both compartments, you will soon notice that the liquid rises in the left compartment and falls in the right side, indicating that water molecules from the right compartment are migrating through the semipermeable membrane and into the left compartment. This migration of the solvent is known as osmotic flow, or simply osmosis .
What is the force that drives the molecules through the membrane? This is a misleading question, because there is no real “force” in the physical sense other than the thermal energies all molecules possess. Osmosis is a consequence of simple statistics: the randomly directed motions of a collection of molecules will cause more to leave a region of high concentration than return to it; the escaping tendency of a substance from a phase increases with its concentration in the phase.
Diffusion and osmotic flow
Suppose you drop a lump of sugar into a cup of tea, without stirring. Initially there will be a very high concentration of dissolved sugar at the bottom of the cup, and a very low concentration near the top. Since the molecules are in random motion, there will be more sugar molecules moving from the high concentration region to the low concentration region than in the opposite direction. The motion of a substance from a region of high concentration to one of low concentration is known as diffusion. Diffusion is a consequence of a concentration gradient (which is a measure of the difference in escaping tendency of the substance in different regions of the solution.
You must clearly understand that there is really no special force on the individual molecules; diffusion is purely a consequence of statistics.
Now take two solutions of differing solvent concentration, and separate them by a semipermeable membrane. Being semipermeable, the membrane is essentially invisible to the solvent molecules, so they diffuse from the high concentration region to the low concentration region just as before. This flow of solvent constitutes osmotic flow, or osmosis.
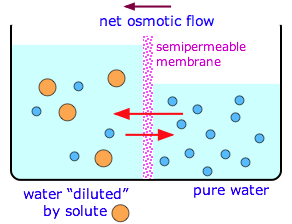
This illustration shows water molecules (blue) passing freely in both directions through the semipermeable membrane, while the larger solute molecules remain trapped in the left compartment, diluting the water and reducing its escaping tendency from this cell, compared to the water in the right side. This results in a net osmotic flow of water from the right side which continues until the increased hydrostatic pressure on the left side raises the escaping tendency of the diluted water to that of the pure water at 1 atm, at which point osmotic equilibrium is achieved.

In the absence of the semipermeable membrane, diffusion would continue until the concentrations of all substances are uniform throughout the liquid phase. With the semipermeable membrane in place, and if one compartment contains the pure solvent, this can never happen; no matter how much liquid flows through the membrane, the solvent in the right side will always be more concentrated than that in the left side. Osmosis will continue indefinitely until we run out of solvent, or something else stops it.
Above left: a nice experiment for students (the illustration does not reveal the results, but see the impressive photo in Section 3 below.) [details]
Osmotic equilibrium and osmotic pressure
 One way to stop osmosis is to raise the hydrostatic pressure on the solution side of the membrane. This pressure squeezes the solvent molecules closer together, raising their escaping tendency from the phase. If we apply enough pressure (or let the pressure build up by osmotic flow of liquid into an enclosed region), the escaping tendency of solvent molecules from the solution will eventually rise to that of the molecules in the pure solvent, and osmotic flow will case. The pressure required to achieve osmotic equilibrium is known as the osmotic pressure. Note that the osmotic pressure is the pressure required to stop osmosis, not to sustain it.
One way to stop osmosis is to raise the hydrostatic pressure on the solution side of the membrane. This pressure squeezes the solvent molecules closer together, raising their escaping tendency from the phase. If we apply enough pressure (or let the pressure build up by osmotic flow of liquid into an enclosed region), the escaping tendency of solvent molecules from the solution will eventually rise to that of the molecules in the pure solvent, and osmotic flow will case. The pressure required to achieve osmotic equilibrium is known as the osmotic pressure. Note that the osmotic pressure is the pressure required to stop osmosis, not to sustain it.
Osmotic pressure and solute concentration
The osmotic pressure Π (Pi) of a solution containing n moles of solute particles in a solution of volume V is given by the van't Hoff equation:
In contrast to the need to employ solute molality to calculate the effects of a non-volatile solute on changes in the freezing and boiling points of a solution, we can use solute molarity to calculate osmotic pressures.
Π = nRT / V
in which R is the gas constant (0.0821 L atm mol–1 K–1) and T is the absolute temperature.
Note that the fraction n/V corresponds to the molarity of a solution of a non-dissociating solute, or to twice the molarity of a totally-dissociated solute such as NaCl. In this context, molarity refers to the summed total of the concentrations of all solute species.
Recalling that Π is the Greek equivalent of P, the re-arranged form ΠV = nRT of the above equation should look familiar. Much effort was expended around the end of the 19th century to explain the similarity between this relation and the ideal gas law, but in fact, the Van’t Hoff equation turns out to be only a very rough approximation of the real osmotic pressure law, which is considerably more complicated and was derived after van't Hoff's formulation. As such, this equation gives valid results only for extremely dilute ("ideal") solutions.
According to the Van't Hoff equation, an ideal solution containing 1 mole of dissolved particles per liter of solvent at 0° C will have an osmotic pressure of 22.4 atm.
Molecular weight determination by osmotic pressure
Since all of the colligative properties of solutions depend on the concentration of the solvent, their measurement can serve as a convenient experimental tool for determining the concentration, and thus the molecular weight, of a solute.
Osmotic pressure is especially useful in this regard, because a small amount of solute will produce a much larger change in this quantity than in the boiling point, freezing point, or vapor pressure. even a 10–6 molar solution would have a measurable osmotic pressure. Molecular weight determinations are very frequently made on proteins or other high molecular weight polymers. These substances, owing to their large molecular size, tend to be only sparingly soluble in most solvents, so measurement of osmotic pressure is often the only practical way of determining their molecular weights.
The experiment is quite simple: pure solvent is introduced into one side of a cell that is separated into two parts by a semipermeable membrane. The polymer solution is placed in the other side, which is enclosed and connected to a manometer or some other kind of pressure gauge. As solvent molecules diffuse into the solution cell the pressure builds up; eventually this pressure matches the osmotic pressure of the solution and the system is in osmotic equilibrium. The osmotic pressure is read from the measuring device and substituted into the van’t Hoff equation to find the number of moles of solute.
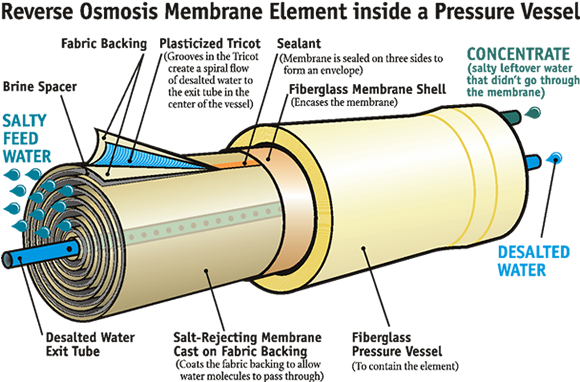
Reverse osmosis
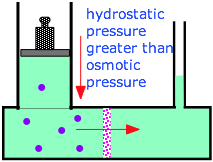 If it takes a pressure of Π atm to bring about osmotic equilibrium, then it follows that applying a hydrostatic pressure greater than this to the high-solute side of an osmotic cell will force water to flow back into the fresh-water side. This process, known as reverse osmosis, is now the major technology employed to desalinate ocean water and to reclaim "used" water from power plants, runoff, and even from sewage. It is also widely used to deionize ordinary water and to purify it for for industrial uses (especially beverage and food manufacture) and drinking purposes.
If it takes a pressure of Π atm to bring about osmotic equilibrium, then it follows that applying a hydrostatic pressure greater than this to the high-solute side of an osmotic cell will force water to flow back into the fresh-water side. This process, known as reverse osmosis, is now the major technology employed to desalinate ocean water and to reclaim "used" water from power plants, runoff, and even from sewage. It is also widely used to deionize ordinary water and to purify it for for industrial uses (especially beverage and food manufacture) and drinking purposes.
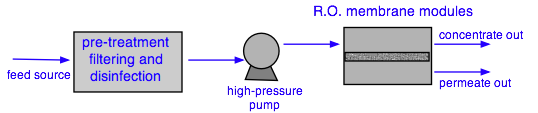
Pre-treatment commonly employs activated-carbon filtration to remove organics and chlorine (which tends to damage RO membranes). Although bacteria are unable to pass through semipermeable membranes, the latter can develop pinhole leaks, so some form of disinfection is often advised.
Membranes for reverse osmosis
The efficiency and cost or RO is critically dependent on the properties of the semipermeable membrane.
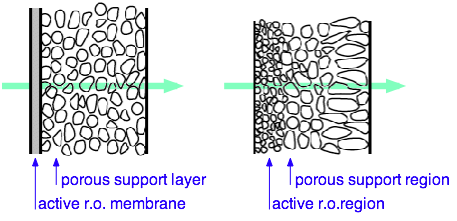

Large-scale RO plants use multiple membrane cartridges. This one, in Tampa Bay FL, supplies desalinated drinking water to 2.4 million residents.
A large plant in Perth, Australia, consumes about 3.8 kWh of energy per cubic meter of water processed.

Many smaller RO units, suitable for home use, can fit under a kitchen sink. [image]
Osmosis of seawater can generate electric power
1 atm is equivalent to
1034 g cm–2, so from the density of water we get
(1034 g cm–2) ÷ (1 g cm–3) = 1034 cm = 10.3 m.
According to Problem Example 2 above, the osmotic pressure of seawater is almost 26 atm. Since a pressure of 1 atm will support a column of water 10.6 m high, this means that osmotic flow of fresh water through a semipermeable membrane into seawater could in principle support a column of the latter by 26 x 10.3 = 276 m (904 ft)!
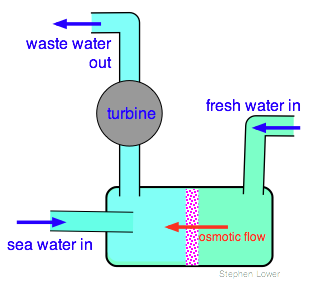 So imagine an osmotic cell in which one side is supplied with fresh water from a river, and the other side with seawater. Osmotic flow of fresh water into the seawater side forces the latter up through a riser containing a turbine connected to a generator, thus providing a constant and fuel-less source of electricity.
So imagine an osmotic cell in which one side is supplied with fresh water from a river, and the other side with seawater. Osmotic flow of fresh water into the seawater side forces the latter up through a riser containing a turbine connected to a generator, thus providing a constant and fuel-less source of electricity.
The key component of such a scheme, first proposed by an Israeli scientist in 1973 and known as pressure-retarded osmosis (PRO) is of course a semipermeable membrane capable of passing water at a sufficiently high rate.
 The world's first experimental PRO plant was opened in 2009 in Norway. Its capacity is only 4 kW, but it serves as proof-in-principle of a scheme that is estimated capable of supplying up to 2000 terawatt-hours of energy worldwide.
The world's first experimental PRO plant was opened in 2009 in Norway. Its capacity is only 4 kW, but it serves as proof-in-principle of a scheme that is estimated capable of supplying up to 2000 terawatt-hours of energy worldwide.
The semipermeable membrane operates at a pressure of about 10 atm and passes 10 L of water per second, generating about 1 watt per m2 of membrane.
PRO is but one form of salinity gradient power that depends on the difference between the salt concentrations in different bodies of water.
Because many plant and animal cell membranes and tissues tend to be permeable to water and other small molecules, osmotic flow plays an essential role in many physiological processes.
Using "normal saline solution" to prevent osmotic disruption of cells
The interiors of cells contain salts and other solutes that dilute the intracellular water. If the cell membrane is permeable to water, placing the cell in contact with pure water will draw water into the cell, tending to rupture it.


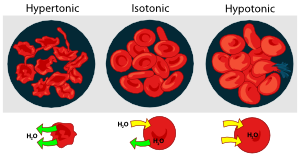 This is easily and dramatically seen if red blood cells are placed in a drop of water and observed through a microscope as they burst. This is the reason that "normal saline solution", rather than pure water, is administered in order to maintain blood volume or to infuse therapeutic agents during medical procedures. [image]
This is easily and dramatically seen if red blood cells are placed in a drop of water and observed through a microscope as they burst. This is the reason that "normal saline solution", rather than pure water, is administered in order to maintain blood volume or to infuse therapeutic agents during medical procedures. [image]
In order to prevent irritation of sensitive membranes, one should always add some salt to water used to irrigate the eyes, nose, throat or bowel.
Normal saline contains 0.91% w/v of sodium chloride, corresponding to 0.154 M, making its osmotic pressure close to that of blood.
Osmotic pressure and food preservation
The drying of fruit, the use of sugar to preserve jams and jellies, and the use of salt to preserve certain meats, are age-old methods of preserving food. The idea is to reduce the water concentration to a level below that in living organisms. Any bacterial cell that wanders into such a medium will have water osmotically drawn out of it, and will die of dehydration. A similar effect is noticed by anyone who holds a hard sugar candy against the inner wall of the mouth for an extended time; the affected surface becomes dehydrated and noticeably rough when touched by the tongue.
In the food industry, what is known as water activity is measured on a scale of 0 to 1, where 0 indicates no water and 1 indicates all water. Food spoilage micro-organisms, in general, are inhibited in food where the water activity is below 0.6. However, if the pH of the food is less than 4.6, micro-organisms are inhibited (but not immediately killed] when the water activity is below 0.85.
|
|
|
Osmosis and diarrhea
 The presence of excessive solutes in the bowel draws water from the intestinal walls, giving rise to diarrhea. This can occur when a food is eaten that cannot be properly digested (as, for example, milk in lactose-intolerant people). The undigested material contributes to the solute concentration, raising its osmotic pressure. The situation is made even worse if the material undergoes bacterial fermentation which results in the formation of methane and carbon dioxide, producing a frothy discharge. [image]
The presence of excessive solutes in the bowel draws water from the intestinal walls, giving rise to diarrhea. This can occur when a food is eaten that cannot be properly digested (as, for example, milk in lactose-intolerant people). The undigested material contributes to the solute concentration, raising its osmotic pressure. The situation is made even worse if the material undergoes bacterial fermentation which results in the formation of methane and carbon dioxide, producing a frothy discharge. [image]
Water transport in plants: osmosis pushes, hydrogen-bonding pulls
Osmotic flow plays an important role in the transport of water from its source in the soil to its release by transpiration from the leaves, it is helped along by hydrogen-bonding forces between the water molecules. Capillary rise is not believed to be a significant factor.
Water enters the roots via osmosis, driven by the low water concentration inside the roots that is maintained by both the active [non-osmotic] transport of ionic nutrients from the soil and by the supply of sugars that are photosynthesized in the leaves. This generates a certain amount of root pressure which sends the water molecules on their way up through the vascular channels of the stem or trunk. But the maximum root pressures that have been measured can push water up only about 20 meters, whereas the tallest trees exceed 100 meters.  Root pressure can be the sole driver of water transport in short plants, or even in tall ones such as trees that are not in leaf. Anyone who has seen apparently tender and fragile plants pushing their way up through asphalt pavement cannot help but be impressed! [knotweed image]
Root pressure can be the sole driver of water transport in short plants, or even in tall ones such as trees that are not in leaf. Anyone who has seen apparently tender and fragile plants pushing their way up through asphalt pavement cannot help but be impressed! [knotweed image]
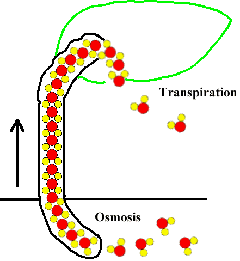 But when taller plants are actively transpiring (losing water to the atmosphere], osmosis gets a boost from what plant physiologists call cohesion tension or transpirational pull. As each H2O molecule emerges from the opening in the leaf it pulls along the chain of molecules beneath it. So hydrogen-bonding is no less important than osmosis in the overall water transport process.
But when taller plants are actively transpiring (losing water to the atmosphere], osmosis gets a boost from what plant physiologists call cohesion tension or transpirational pull. As each H2O molecule emerges from the opening in the leaf it pulls along the chain of molecules beneath it. So hydrogen-bonding is no less important than osmosis in the overall water transport process.
If the soil becomes dry or saline, the osmotic pressure outside the root becomes greater than that inside the plant, and the plant suffers from “water tension”, i.e., wilting.
Osmosis and evolution: Do fish drink water? Do they pee?
The following section is a bit long, but for those who are interested in biology it offers a beautiful example of how the constraints imposed by osmosis have guided the evolution of ocean-living creatures into fresh-water species . It concerns ammonia NH3, a product of protein metabolism that is generated within all animals, but is highly toxic and must be eliminated.
Marine invertebrates (those that live in seawater) are covered in membranes that are fairly permeable to water and to small molecules such as ammonia. So water can diffuse in either direction as required, and ammonia can diffuse out as quickly as it forms. Nothing special here.
But invertebrates that live in fresh water have a problem: the salt concentrations within their bodies are around 1%, much greater than in fresh water. For this reason they have evolved surrounding membranes that are largely impermeable to salts (to prevent their diffusion out of the body) and to water (to prevent osmotic flow in.) But these organisms must also be able to exchange oxygen and carbon dioxide with their environment. The special respiratory organs (gills) that mediate this process, as a consequence of being permeable to these two gases, will also allow water molecules (whose sizes are comparable to those of the respiratory gases) to pass through. In order to protect fresh-water invertebrates from the disastrous effects of unlimited water inflow through the gill membranes, these animals possess special excretory organs that expel excess water back into the environment. Thus in such animals, there is a constant flow of water passing through the body. Ammonia and other substances that need to be excreted are taken up by this stream which constitutes a continual flow of dilute urine.
Fishes fall into two general classes: most fish have bony skeletons and are known as teleosts. Sharks and rays have cartilage instead of bones, and are called elasmobranchs.
For the teleosts that live in fresh water, the situation is very much the same as with fresh-water invertebrates; they take in and excrete water continuously.
Marine teleosts have a more difficult problem. Their gills are permeable to water, as are those of marine invertebrates. But the salt content of seawater (about 3%), being higher than the about 1% in the fish’s blood, would draw water out of the fish. Thus these animals are constantly losing water, and would be liable to desiccation if water could freely pass out of their gills. Some does, of course, and with it goes most of its nitrogen in the form of NH3.
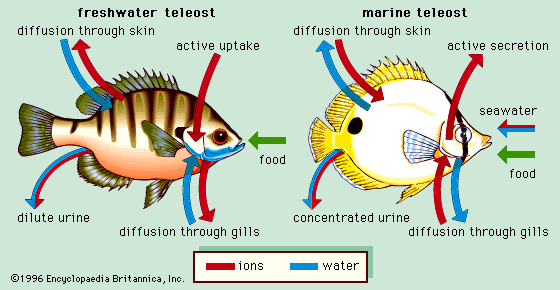
Thus most of the waste nitrogen exits not through the usual excretory organs as with most vertebrates, but through the gills. But in order to prevent excessive loss of water, the gills have reduced permeability to this water, and with it, to comparably-sized NH3. So in order to prevent ammonia toxicity, the remainder of it is converted to a non-toxic substance (trimethylamine oxide (CH3)3NO) which is excreted via the kidneys.
The marine elasmobranchs solve the loss-of-water problem in another way: they convert waste ammonia to urea (NH3)2CO which is highly soluble and non-toxic. Their kidneys are able to control the quantity of urea excreted so that their blood retains about 2-2.5 percent of this substance. Combined with the 1 percent of salts and other substances in their blood, this raises the osmotic pressure within the animal to slightly above that of seawater, Thus the same mechanism that protects them from ammonia poisoning also ensures them an adequate water supply.
The fresh-water elasmobranchs, which are believed to be descended from their marine relatives, also convert ammonia into urea, but their kidneys excrete nearly all of it.
Further evidence that detoxification of ammonia evolved primarily as an adaptation to limited water supply is seen in many other organisms. For example, tadpoles excrete ammonia directly into the water in which they hatch, but when they develop into frogs, the kidneys excrete urea. Humans, as animals that have descended from reptiles, retain the mechanism that converts ammonia into urea.





